Luonnolliset geometriset kuviot tai kuviot näkyvät toistuvina muotoina, joita voidaan joskus kuvata tai esittää matemaattisilla malleilla.
Geometriaa luonnossa ja elämässä on monia muotoja, kuten symmetriaa, spiraalia tai a altoja.
Historia
Ensimmäistä kertaa antiikin kreikkalaiset filosofit ja tiedemiehet - Pythagoras, Empedokles ja Platon - ottivat esiin kysymyksiä geometriasta luonnossa. Analysoimalla esimerkkejä ennustettavissa olevista tai ihanteellisista geometrisista muodoista kasveissa ja eläimissä he yrittivät osoittaa järjestystä ja symmetriaa luonnossa.
Nykyaikaiset yritykset tutkia geometriaa luonnossa alkoivat 1800-luvulla belgialaisen fyysikon Joseph Plateaun ponnisteluilla. Hän kehitti käsitteen saippuakuplan vähimmäispinnasta. Ensimmäiset modernit yritykset keskittyivät ensin ihanteellisten ja ennustettavien geometristen muotojen esittelyyn ja sitten suuntautuivat sellaisten mallien kehittämiseen, jotka ennustavat geometrian esiintymistä ja ilmenemistä luonnossa.
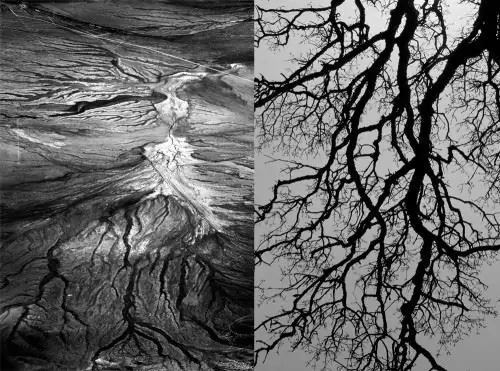
1900-luvulla matemaatikko Alan Turing työskenteli morfogeneesin mekanismien parissa, mikä selittää esiintymisen eläimissäerilaisia kuvioita, raitoja, täpliä. Hieman myöhemmin biologi Aristide Lindenmeier yhdessä matemaatikon Benoit Mandelbrotin kanssa viimeistelevät työn matemaattisista fraktaaleista, jotka toistivat joidenkin kasvien, mukaan lukien puiden, kasvutapoja.
Tiede
Modernitieteet (matematiikka, fysiikka ja kemia) yrittävät teknologioiden ja mallien avulla paitsi selittää, myös ennustaa luonnossa esiintyviä geometrisia kuvioita.
Monien elävien organismien, kuten riikinkukon, hummingbirdin ja simpukoiden muoto ja väri eivät ole vain kauniita, vaan myös geometrisesti oikein, mikä herättää tutkijoiden uteliaisuutta. Luonnossa havaitsemamme kauneus voidaan aiheuttaa luonnollisesti, matemaattisesti.
Matematiikan havaitut luonnolliset kuviot selittyvät kaaosteorialla, joka toimii spiraaleiden ja fraktaalien kanssa. Tällaiset kuviot noudattavat fysiikan lakeja, ja lisäksi fysiikka ja kemia ennustavat abstraktia matematiikkaa käyttäen kiteiden muotoja, sekä luonnollisia että keinotekoisia.
Biologia selittää geometrian luonnossa luonnollisella valinnalla, jossa sellaiset säännölliset ominaisuudet kuten raidat, täplät, kirkkaat värit voidaan selittää peittämisen tai signaalien lähettämisen tarpeella.
Kaaviotyypit
Luonnossa on monia toistuvia kuvioita, jotka esiintyvät erilaisissa geometrisissa muodoissa. Luonnon geometrian perussäännönmukaisuuden tyypit, valokuvat ja niiden kuvaukset löydät alta.
Symmetria. Tämä geometrinen muoto on yksi yleisimmistä luonnossa. Yleisin eläimilläpeilisymmetria - perhoset, kovakuoriaiset, tiikerit, pöllöt. Sitä löytyy myös kasveista, kuten vaahteran lehdistä tai orkidean kukista. Lisäksi symmetrinen geometria luonnossa voi olla säteittäistä, viisisäteistä tai kuusinkertaista, kuten lumihiutaleita.

Fraktaalit. Matematiikassa nämä ovat itseään samank altaisia konstruktioita, jotka ovat äärettömiä. Luonnossa on mahdotonta havaita tällaista loputonta itseään toistuvaa muotoa, joten fraktaalikuvioiden likiarvoja kutsutaan luonnossa geometrisiksi fraktaaleiksi. Tällaista geometriaa voi havaita luonnossa saniaisten lehdissä, parsakaalissa, ananashedelmissä.
Spiraalit. Nämä muodot ovat erityisen yleisiä nilviäisten ja etanoiden keskuudessa. Tutkijat tarkkailevat avaruudessa spiraalimuotoja, esimerkiksi spiraaligalakseja. Spiraalia kutsutaan Fibonaccin kultaiseksi leikkaukseksi.

Meanders. Matematiikassa dynaamisten järjestelmien satunnaisuus ilmenee luonnossa mutkien ja virtausten muodossa. Luonnongeometria on katkenneen tai melko kaarevan viivan, kuten joen virtauksen, muodossa.
Aallot. Ne johtuvat häiriöistä ja ilman liikkeistä, tuulivirroista, jotka leviävät sekä ilman että veden kautta. Luonnossa nämä eivät ole vain meren a altoja, vaan myös aavikon dyynejä, jotka voivat muodostaa geometrisia muotoja - viivoja, puolikuuja ja paraabeleja.
Mosaiikki. Luotu toistamalla samoja elementtejä pinnalla. Villieläinten mosaiikkigeometria löytyy mehiläisistä: ne rakentavathunajakennojen pesä - toistuvat solut.

Kuvioiden muodostuminen
Biologiassa geometrisen värin muodostuminen johtuu luonnollisen valinnan prosessista. 1900-luvun puolivälissä Alan Turing onnistui kuvailemaan mekanismia täplien ja raitojen esiintymiseen eläinten värissä - hän kutsui sitä reaktio-diffuusiomalliksi. Tietyt kehon solut sisältävät geenejä, joita säätelevät kemialliset reaktiot. Morfogeeni johtaa ihoalueiden muodostumiseen tummilla pigmenteillä (täplät ja raidat). Jos morfogeeniä on kaikissa ihosoluissa - saadaan pantterin väri, jos se esiintyy epätasaisesti - tavallinen täplikäs leopardi.






