Fysiikkaa opiskellessa 10. luokalla huomioidaan dipolit. Mitä tämä käsite tarkoittaa ja millä kaavoilla se lasketaan?
Esittely
Jos asetat dipolin tasaisen sähkökentän tilaan, voit esittää sen voimalinjoina. Dipoli on järjestelmä, jossa on kaksi parametriltaan identtistä varausta, mutta ne ovat vastakkaisia pistevarauksia. Lisäksi niiden välinen etäisyys on paljon pienempi kuin etäisyys mihin tahansa dipolikentän pisteeseen. Dipolimomentin käsitettä opiskellaan sähködynamiikan koulukurssilla (luokka 10).
Dipolin akseli on suora viiva, joka kulkee molempien varausten pisteiden läpi. Dipolivarsi on vektori, joka yhdistää varauksen ja samalla siirtyy negatiivisesti varautuneista hiukkasista positiivisesti varautuneisiin hiukkasiin. Sähködipolille on ominaista sellaisen tilan olemassaolo kuin dipoli tai sähkömomentti.
Määritelmän mukaan dipolimomentti on vektori, joka on numeerisesti yhtä suuri kuin dipolivarauksen ja sen haaran tulo. Lisäksi se ohjataan yhdessä dipolin olkapään kanssa. Kun voimien summa on yhtä suuri, laskemme hetken arvon. Kulalle, joka vallitsee dipolimomentin ja välilläsähkökentän suuntaus, mekaanisen momentin läsnäolo on ominaista.
Usein ihmisten on vaikea laskea dipolirakenteeseen vaikuttavaa moduulia. Tässä on otettava huomioon kulman "Alfa" laskemisen erityispiirteet. Tiedetään, että dipoli poikkeaa tasapainoisesta asennosta. Mutta itse dipolimomentilla on palauttava luonne, sillä se pyrkii olemaan liikkeessä.
Laskelmat
Kun tämä dipolimomentti asetetaan epähomogeenisen sähkökentän väliaineeseen, syntyy väistämättä voima. Tällaisessa ympäristössä voimien summan indikaattorit eivät ole nolla. Näin ollen on olemassa voimia, jotka vaikuttavat pisteluonteiseen dipolimomenttiin. Dipolivarren koko on paljon pienempi.
Kaava voidaan kirjoittaa näin: F=q (E2 - E1)=qdE, missä d on sähkökentän differentiaali.
Etsi tutkittavan fyysisen käsitteen ominaisuuksia
Katsotaanpa aihetta lisää. Sen määrittämiseksi, mikä on sähkökentän ominaisuus, jos se luodaan varausjärjestelmällä ja lokalisoidaan pieneen tilaan, on tarpeen tehdä useita laskelmia. Esimerkkinä ovat atomit ja molekyylit, joiden koostumuksessaan on sähköisesti varautuneita ytimiä ja elektroneja.
Jos on tarpeen etsiä kenttää etäisyydeltä, joka on suurempi kuin mitat, jotka muodostavat alueen, jossa hiukkaset sijaitsevat, käytämme useita tarkkoja kaavoja, jotka ovat erittäin monimutkaisia. On mahdollista käyttää yksinkertaisempaalikimääräisiä lausekkeita. Oletetaan, että sähkökentän muodostumiseen osallistuvat varausten pistejoukot qk. Ne sijaitsevat pienessä tilassa.
Kentän ominaisuuden laskennan suorittamiseksi on sallittua yhdistää kaikki järjestelmän varaukset. Tällaista järjestelmää pidetään pistevarauksena Q. Suuruusindikaattorit ovat niiden varausten summa, jotka olivat alkuperäisessä järjestelmässä.
Maksujen sijainti
Kuvitellaan, että latauksen sijainti on merkitty missä tahansa paikassa, jossa maksujärjestelmä qk sijaitsee. Muutoksia tehtäessä, jos sillä on pienellä alueella ilmaistut rajat, tällainen vaikutus on mitätön, näkökulmasta kentälle lähes huomaamaton. Sähkökentän voimakkuuden ja potentiaalin likimääräisten rajojen sisällä määritykset tehdään perinteisin kaavoin.
Kun järjestelmän kokonaislatauksen summa on nolla, esitetyn likiarvon parametrit näyttävät karkeilta. Tämä antaa aiheen päätellä, että sähkökenttä yksinkertaisesti puuttuu. Jos on tarpeen saada tarkempi likiarvo, kerää mielessään erilliset ryhmät tarkasteltavan järjestelmän positiivisia ja negatiivisia varauksia.
Jos niiden "keskipisteet" siirtyvät suhteessa muihin, tällaisen järjestelmän kenttäparametreja voidaan kuvata kentällä, jossa on kaksi pistevarausta, jotka ovat yhtä suuret ja vastakkaiset etumerkillä. On huomattava, että he ovat siirtyneet muihin nähden. TarjotaVarausjärjestelmän tarkempaa karakterisointia varten tämän approksimoinnin parametrien suhteen on tarpeen tutkia dipolin ominaisuuksia sähkökentässä.
Termin esittely
Palataanpa määritelmään. Sähködipoli on määritelmä järjestelmälle, jossa on kaksi pistevarausta. Niillä on sama koko ja päinvastaiset merkit. Lisäksi tällaiset kyltit sijaitsevat pienillä etäisyyksillä muihin kylteihin nähden.
Voit laskea dipolin avulla luodun prosessin ominaisuuden, ja sitä edustavat kaksi pistevarausta: +q ja −q, ja ne sijaitsevat a-etäisyydellä muihin nähden.

Laskentajärjestys
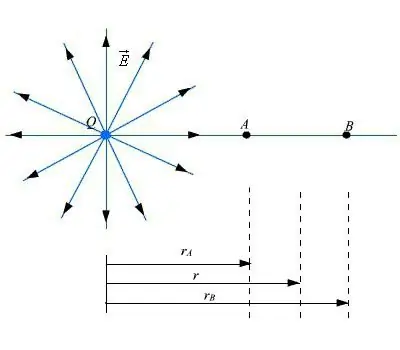
Aloitetaan laskemalla potentiaali ja intensiteetti, joka dipolilla on aksiaalisella pinnallaan. Tämä on suora viiva, joka kulkee kahden latauksen välillä. Edellyttäen, että piste A sijaitsee etäisyydellä, joka on yhtä suuri kuin r suhteessa dipolin keskiosaan, ja jos se on r >> a, tässä pisteessä olevan kenttäpotentiaalin superpositioperiaatteen mukaisesti on järkevää käytä lauseketta sähködipolin parametrien laskemiseen.
voimakkuusvektorin suuruus lasketaan superpositioperiaatteella. Kenttävoimakkuuden laskemiseen käytetään potentiaalin ja kentänvoimakkuuden suhteen käsitettä:
Ex=−Δφ /Δx.
Tällaisissa olosuhteissa intensiteettivektorin suunta ilmaistaan pituussuunnassa suhteessa dipoliakseliin. Sen moduulin laskemiseen käytetään vakiokaavaa.
Tärkeääselvennykset
Tulee ottaa huomioon, että sähködipolikentän heikkeneminen tapahtuu nopeammin kuin se kokee pistevarauksen. Dipolikenttäpotentiaalin vaimeneminen on kääntäen verrannollinen etäisyyden neliöön ja kentänvoimakkuus on kääntäen verrannollinen etäisyyden kuutioon.
Samank altaisilla, mutta monimutkaisemmilla menetelmillä dipolin potentiaalin ja kentänvoimakkuuden parametrit löydetään mieliv altaisista pisteistä, joiden sijaintiparametrit määritetään sellaisella laskentamenetelmällä napakoordinaateina: etäisyys sähködipolin (r) ja kulman (θ) keskipiste.
Laskenta jännitysvektorin avulla
Intensiteettivektorin E käsite on jaettu kahteen kohtaan:
- Säteittäinen (Er), joka on suunnattu pituussuunnassa suhteessa suoraan.
- Tällainen suora yhdistää määritellyn pisteen ja dipolin keskikohdan siihen nähden kohtisuoraan Eθ.
Tämä kunkin komponentin hajoaminen on suunnattu muutoksen kulkua pitkin, joka tapahtuu kaikkien tarkkailtavan pisteen koordinaattien kanssa. Löydät sen suhteesta, joka yhdistää kentänvoimakkuusindikaattorit mahdollisiin muutoksiin.
Löydettäessä vektorikomponenttia kentänvoimakkuudesta, on tärkeää selvittää mahdollisten muutosten välinen suhde, joka syntyy havaintopisteen siirtymisestä vektorien suuntaan.
Laske kohtisuora komponentti
Kun valmisTässä menettelyssä on tärkeää ottaa huomioon, että suuruuden lauseke pienellä kohtisuoralla siirtymällä määritetään muuttamalla kulmaa: Δl=rΔθ. Tämän kenttäkomponentin suuruusparametrit ovat yhtä suuret.
Kun suhde on saatu, on mahdollista määrittää sähködipolin kenttä mieliv altaisessa pisteessä ja muodostaa kuva tämän kentän voimalinjoista.
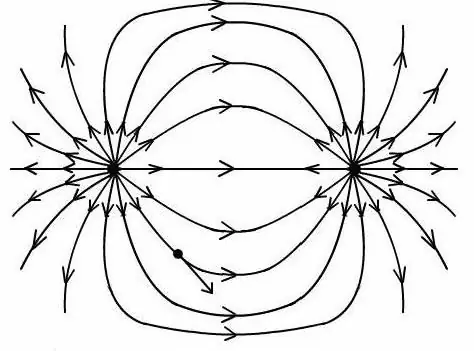
On tärkeää ottaa huomioon, että kaikki kaavat dipolin potentiaalin ja kentänvoimakkuuden määrittämiseksi toimivat vain yhden dipolivarauksen arvojen ja niiden välisen etäisyyden tulolla.
Dipolihetki
Kuvatun työn nimi on täydellinen kuvaus sähköisistä ominaisuuksista. Sen nimi on "järjestelmän dipolimomentti".
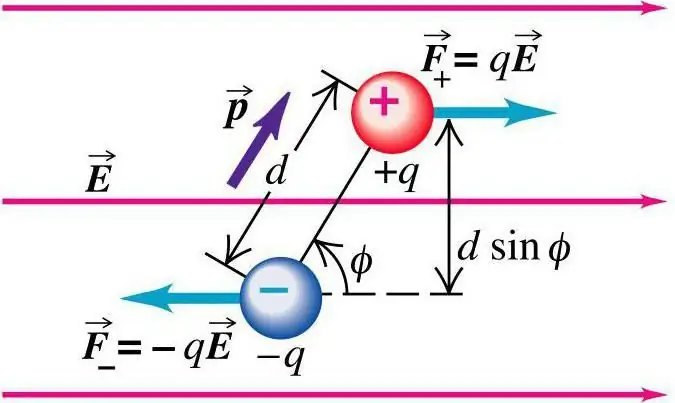
Dipolin, joka on pistevarausten järjestelmä, määritelmästä voidaan todeta, että sille on ominaista aksiaalinen symmetria, kun akseli on suora, joka kulkee useiden varausten läpi.
Asettaaksesi koko dipolin ominaiskäyrän, osoita akselin suuntaussuunta. Laskelmien yksinkertaistamiseksi voidaan määrittää dipolimomenttivektori. Sen suuruuden arvo on yhtä suuri kuin dipolimomentin suuruus, ja suuntavektori eroaa sen ja dipolin akselin yhteensattumisesta. Joten p=qa, jos a on sen vektorin suunta, joka yhdistää dipolin negatiiviset ja positiiviset varaukset.
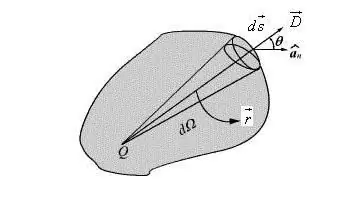
Tällaisen dipolin ominaisuuden käyttö on kätevää ja mahdollistaa useimmissa tapauksissa kaavan yksinkertaistamisen ja muodon antamisenvektori. Kuvaus dipolikentän potentiaalista mieliv altaisen suunnan pisteessä kirjoitetaan vektorin muodossa.
Sellaisten käsitteiden käyttöönotto kuin dipolin ominaisuusvektori ja sen dipolimomentti voidaan toteuttaa yksinkertaistetulla mallilla − pistevarauksella yhtenäisessä kentässä, joka sisältää varausjärjestelmän, jonka geometriset mitat ovat ei tarvitse ottaa huomioon, mutta on tärkeää tietää dipolimomentti. Tämä on edellytys laskelmien suorittamiselle.
Miten dipoli käyttäytyy
Dipolin käyttäytyminen voidaan nähdä tällaisen tilanteen esimerkissä. Kahden pistevarauksen sijainnilla on kiinteä etäisyys toisiinsa nähden. Ne asetettiin tasaisen sähkökentän dipolin olosuhteisiin. Teki havaintoja prosessista. Fysiikan (elektrodynamiikan) tunneilla tätä käsitettä tarkastellaan yksityiskohtaisesti. Kentältä lataukseen suoritetaan voimien toiminta:
F=±qE
Ne ovat suuruudeltaan yhtä suuret ja suunn altaan vastakkaiset. Dipoliin vaikuttavan kokonaisvoiman indikaattori on nolla. Koska tällainen voima vaikuttaa useisiin pisteisiin, kokonaismomentti on:
M=Fa sin a=qEa sin a=pE sin a
jossa α on kulma, joka yhdistää kentänvoimakkuusvektorit ja dipolimomenttivektorit. Voimamomentin läsnäolon vuoksi järjestelmän dipolimomentti pyrkii palaamaan sähkökentän voimakkuusvektorin suuntiin.
Sähködipoli on käsite, joka on tärkeää ymmärtää selvästi. Voit lukea siitä lisää Internetistä. Myös se voiopiskella fysiikan tunneilla koulussa 10 luokalla, kuten puhuimme edellä.






