Kun fysiikassa tutkitaan kappaleiden mekaanista liikettä avaruudessa, ne ottavat aina huomioon tuloksena olevan kiihtyvyyden. Pohditaan artikkelissa, mitä kiihtyvyys on ja miten se ilmaistaan fysiikassa, ja ratkaistaan myös yksinkertainen tehtävä tämän arvon laskemiseksi.
Mitä on kiihtyvyys ja mitkä ovat sen tyypit?
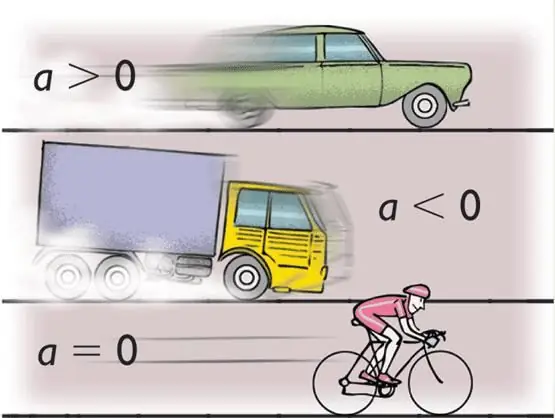
Ymmärrä kiihtyvyyden alla arvo, jonka merkitys on kehon nopeuden muutosnopeus. Matemaattisesti tämä määritelmä on kirjoitettu seuraavasti:
a=dv/dt.
Jos nopeuden aikafunktio tunnetaan, riittää sen ensimmäinen derivaatta, jotta voidaan laskea kiihtyvyys tietyllä hetkellä.
Fysiikassa kiihtyvyyskirjain on pieni latinalainen a. Tämä on kuitenkin niin kutsuttu lineaarinen kiihtyvyys, joka mitataan yksiköissä m/s2. Sen lisäksi on myös kulmakiihtyvyyttä. Se näyttää muutoksen kulmanopeudessa ja ilmaistaan yksiköissä rad/s2. Tämän tyyppinen kiihtyvyys on merkitty kreikkalaisella pienellä kirjaimella α (alfa). Joskuskirjainta ε (epsilon) käytetään merkitsemään sitä.
Jos keho liikkuu kaarevaa liikerataa pitkin, kokonaiskiihtyvyys jakautuu kahteen osaan: tangentiaaliseen (määrittää nopeuden muutoksen suuruusluokissa) ja normaaliksi (määrittää nopeuden suunnan muutoksen). Tämän tyyppiset kiihtyvyydet on merkitty myös kirjaimilla a, mutta käyttämällä vastaavia indeksejä: at ja a. Normaalia kutsutaan usein sentripetaaliksi ja tangentiaaliksi tangentiksi.
Lopuksi on olemassa toisenlainen kiihtyvyys, joka tapahtuu, kun kappaleet putoavat vapaasti planeetan gravitaatiokentässä. Se on merkitty kirjaimella g.
Kiihtyvyyden fysiikan ongelma
On tunnettua, että keho liikkuu suorassa linjassa. Sen nopeus ajan kuluessa määräytyy seuraavan lain mukaan:
v=2t2-t+4.
On tarpeen laskea kiihtyvyys, joka keholla on hetkellä t=2,5 sekuntia.
A:n määritelmän mukaisesti saamme:
a=dv/dt=4t - 1.
Toisin sanoen arvo a riippuu lineaarisesti ajasta. On mielenkiintoista huomata, että alkuhetkellä (t=0) kiihtyvyys oli negatiivinen, eli suunnattu nopeusvektoria vastaan. Saamme vastauksen ongelmaan korvaamalla t=2,5 sekuntia tähän yhtälöön: a=9 m/s2.






