Mitä vanhemmaksi opiskelijat tulevat, sitä enemmän tarvitaan nopeutta yksinkertaisten ongelmien ratkaisemisessa. Kokeissa ei anneta paljon aikaa yksinkertaisten esimerkkien tai ongelmien ratkaisemiseen pitkään aikaan. Kuinka löytää neliön diagonaali nopeasti ja helposti? Tätä opetetaan lapsille kahdeksannesta luokasta lähtien. Tämä artikkeli näyttää kaksi tapaa - toinen on pidempi, toinen nopeampi.
Kuinka lasketaan neliön diagonaali?
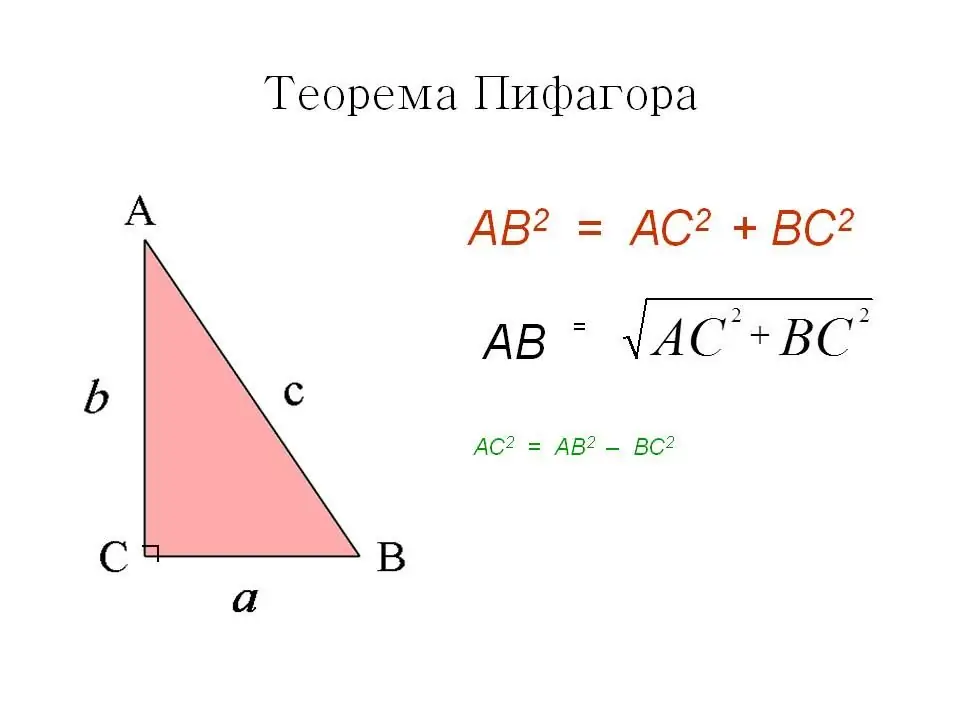
Ensimmäinen tapa on hyvin tunnettu ja tuttu Pythagoraan lause. Neliössä kaikki kulmat ovat suorat, mikä tarkoittaa, että diagonaali jakaa sen kahdeksi yhtä suureksi suorakulmaiseksi kolmioksi ja on itse niiden hypotenuusa. Pythagoraan lauseen mukaan hypotenuusan neliö on yhtä suuri kuin jalkojen neliöiden summa.

Toinen tapa on yksinkertainen kaava, joka on ainutlaatuinen neliöille, ja sinun tarvitsee vain muistaa se. Kuten tiedät, neliön kaikki sivut ovat yhtä suuret, ja siksi matemaatikot ovat laskeneet seuraavan kaavan sen diagonaalin löytämiseksi: se on yhtä suuri kuin sivun ja kahden juuren tulo.
Tietenkin on parasta vain muistaa neliön diagonaalin pituuden kaava ja käyttää sitä aina, koska se on paljon nopeampaa ja kätevämpää. Tämä tuntuu erityisesti ratkaistaessa tehtäviä kirjaimellisessa muodossa, jossa kokonaisten suurten juurilausekkeiden sijaan pärjäät vain yhdellä tuotteella.
Esimerkki
Otetaan esimerkiksi neliö 6 x 6, eli jonka sivu on kuusi senttimetriä.
Ensimmäisen menetelmän mukaan: olkoon diagonaali C ja sivu A.
Sitten saamme, että C=√A^2+A^2 tai C=√2A^2.
Kirjoitetaan se numeromuodossa: С=√36 + 36. Saimme √72, joka on 3√8 tai 6√2.
Ja nyt etsitään sama diagonaali, mutta toisella menetelmällä: C=A√2 tai numeromuodossa: 6√2
Nyt näet kuinka paljon toinen menetelmä on nopeampi, helpompi ja mikä tärkeintä - tehokkaampi, varsinkin näin helpoissa tehtävissä, koska jokainen minuutti on arvokas kokeessa!
Neliön diagonaalien muut ominaisuudet
Sen lisäksi, että osaat löytää neliön lävistäjät, sinun on myös tiedettävä niiden ominaisuudet. Tärkeimmät ovat:
- Dagonaalit ovat keskenään yhtä suuret ja leikkauspiste jaetaan puoliksi.
- Ne muodostavat suoran kulman, kun ne leikkaavat.
- Jaa neliö yhtä suuriin kolmioihin.
Johtopäätös
Kysymyksen neliön diagonaalien laskemisesta kysyvät yleensä opiskelijat, jotka eivät osanneet tästä aiheesta koulussa. Kaikkien pitäisi kuitenkin tietää tällaiset matematiikan perussäännöt! On toivottavaa ratkaista mahdollisimman nopeasti, ja tämä edellyttää lyhennettyjen kaavojen tuntemista. Kaikki tämä on erittäin yksinkertaista ja helppoa, muttaSamalla se on perusta monimutkaisempien ongelmien ratkaisemiselle tulevaisuudessa. Ja tärkeä osa tätä pohjaa on neliö.






