Termodynamiikassa, kun tutkitaan siirtymiä järjestelmän alkutilasta lopputilaan, on tärkeää tietää prosessin lämpövaikutus. Lämpökapasiteetin käsite liittyy läheisesti tähän vaikutukseen. Tässä artikkelissa pohditaan kysymystä siitä, mitä tarkoitetaan kaasun isokorisella lämpökapasiteetilla.
Ihanteellinen kaasu
Ihanteellinen kaasu on kaasu, jonka hiukkasia pidetään aineellisina pisteinä, eli niillä ei ole mittoja, mutta niillä on massaa ja jossa kaikki sisäinen energia koostuu yksinomaan molekyylien liikkeen liike-energiasta ja atomit.
Mikään todellinen kaasu ei ihannetapauksessa koskaan täytä kuvattua mallia, koska sen hiukkasilla on edelleen joitain lineaarisia mittoja ja ne ovat vuorovaikutuksessa toistensa kanssa käyttämällä heikkoja van der Waalsin sidoksia tai muun tyyppisiä kemiallisia sidoksia. Matalissa paineissa ja korkeissa lämpötiloissa molekyylien väliset etäisyydet ovat kuitenkin suuret ja niiden liike-energia ylittää potentiaalisen energian kymmeniä kertoja. Kaikki tämä mahdollistaa ihanteellisen mallin soveltamisen todellisille kaasuille suurella tarkkuudella.
Kaasun sisäinen energia
Jokaisen järjestelmän sisäinen energia on fysikaalinen ominaisuus, joka on yhtä suuri kuin potentiaalisen ja liike-energian summa. Koska ideaalikaasuissa potentiaalienergia voidaan jättää huomiotta, voimme kirjoittaa niille yhtäläisyyden:
U=Ek.
Missä Ek on kineettisen järjestelmän energia. Käyttämällä molekyylikineettistä teoriaa ja soveltamalla universaalia Clapeyron-Mendeleevin tilayhtälöä ei ole vaikeaa saada lauseke U:lle. Alla on kirjoitettu:
U=z/2nRT.
Tässä T, R ja n ovat absoluuttinen lämpötila, kaasuvakio ja aineen määrä, vastaavasti. Z-arvo on kokonaisluku, joka ilmaisee kaasumolekyylin vapausasteiden lukumäärän.
Isobaarinen ja isokoorinen lämpökapasiteetti
Fysiikassa lämpökapasiteetti on lämpömäärä, joka on syötettävä tutkittavaan järjestelmään, jotta se lämmittää sen yhdellä kelvinillä. Myös käänteinen määritelmä pitää paikkansa, eli lämpökapasiteetti on se lämmön määrä, jonka järjestelmä vapauttaa, kun se jäähtyy yhdellä kelvinillä.
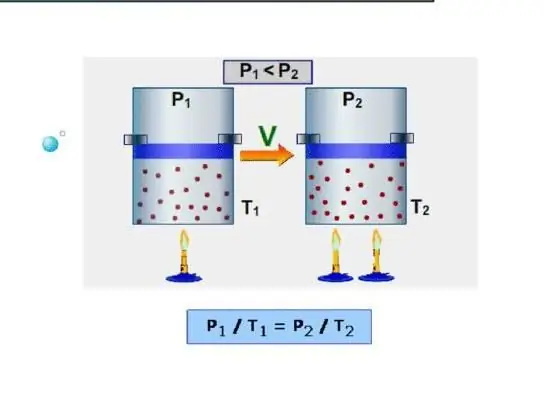
Helppoin tapa järjestelmälle on määrittää isokorinen lämpökapasiteetti. Se ymmärretään lämpökapasiteetiksi vakiotilavuudessa. Koska järjestelmä ei toimi tällaisissa olosuhteissa, kaikki energia kuluu sisäisten energiavarastojen lisäämiseen. Merkitään isokorinen lämpökapasiteetti symbolilla CV, jolloin voimme kirjoittaa:
dU=CVdT.
Toisin sanoen sisäisen energian muutosjärjestelmä on suoraan verrannollinen sen lämpötilan muutokseen. Jos verrataan tätä lauseketta edellisessä kappaleessa kirjoitettuun yhtäläisyyteen, niin saamme ideaalisessa kaasussa kaavan CV:
СV=z/2nR.
Tätä arvoa on hankala käyttää käytännössä, koska se riippuu järjestelmän aineen määrästä. Siksi otettiin käyttöön isokorisen ominaislämpökapasiteetin käsite, eli arvo, joka lasketaan joko 1 moolia kaasua tai 1 kg:aa kohti. Merkitään ensimmäinen arvo symbolilla CV, toinen - symbolilla CV m. Voit kirjoittaa heille seuraavat kaavat:
CV=z/2R;
CVm=z/2R/M.
Tässä M on moolimassa.
Isobaarinen on lämpökapasiteetti, samalla kun järjestelmässä säilyy vakiopaine. Esimerkki tällaisesta prosessista on kaasun paisuminen sylinterissä männän alla, kun sitä kuumennetaan. Toisin kuin isokoorisessa prosessissa, isobarisessa prosessissa järjestelmään syötetty lämpö kuluu sisäisen energian lisäämiseen ja mekaanisen työn suorittamiseen, eli:
H=dU + PdV.
Isobarisen prosessin entalpia on isobarisen lämpökapasiteetin ja järjestelmän lämpötilan muutoksen tulos, eli:
H=CPdT.
Jos tarkastelemme laajenemista vakiopaineessa 1 moolissa kaasua, termodynamiikan ensimmäinen pääsääntö kirjoitetaan seuraavasti:
CPdT=CV dT + RdT.
Viimeinen termi saadaan yhtälöstäClapeyron-Mendelejev. Tästä yhtälöstä seuraa isobarisen ja isokorisen lämpökapasiteetin välinen suhde:
CP=CV + R.
Ideaaliselle kaasulle ominaismoolilämpökapasiteetti vakiopaineessa on aina suurempi kuin vastaava isokooriominaisuus, jonka R=8, 314 J/(molK).
Molekyylien vapausasteet ja lämpökapasiteetti
Kirjoitetaan uudelleen kaava molaariselle isokoriselle lämpökapasiteetille:
CV=z/2R.
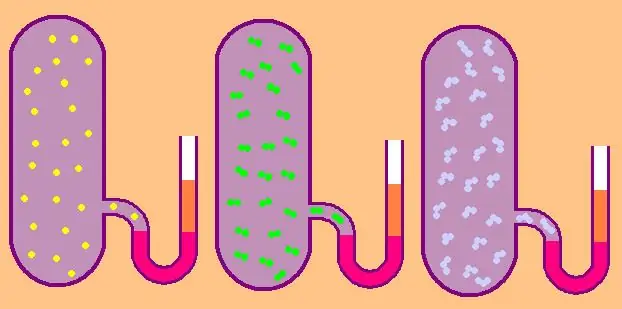
Monaatomisen kaasun tapauksessa arvo z=3, koska atomit avaruudessa voivat liikkua vain kolmeen itsenäiseen suuntaan.
Jos puhumme kaasusta, joka koostuu diatomisista molekyyleistä, esimerkiksi hapesta O2 tai vedystä H2, niin translaatioliikkeen lisäksi nämä molekyylit voivat silti pyöriä kahden keskenään kohtisuoran akselin ympäri, eli z on yhtä suuri kuin 5.
Jos haluat monimutkaisemmat molekyylit, käytä z=6. määrittääksesi CV






