Jokainen ihminen kohtaa elämänsä aikana kappaleita, jotka ovat jossakin kolmesta aineen aggregaattitilasta. Yksinkertaisin tutkittava aggregaatiotila on kaasu. Artikkelissa tarkastellaan ideaalisen kaasun käsitettä, annetaan järjestelmän tilayhtälö ja kiinnitetään myös huomiota absoluuttisen lämpötilan kuvaukseen.
Aineen olomuoto
Jokaisella opiskelijalla on hyvä käsitys siitä, mistä ainetilasta hän puhuu, kun hän kuulee sanan "kaasu". Tämä sana ymmärretään kappaleeksi, joka pystyy ottamaan minkä tahansa sille tarjotun tilavuuden. Se ei pysty säilyttämään muotoaan, koska se ei voi vastustaa pienintäkään ulkoista vaikutusta. Kaasu ei myöskään säilytä tilavuutta, mikä erottaa sen paitsi kiinteistä aineista myös nesteistä.
Nesteen tapaan kaasu on nestemäinen aine. Kiinteiden kappaleiden liikkeessä kaasuissa jälkimmäiset estävät tätä liikettä. Tuloksena olevaa voimaa kutsutaan vastukseksi. Sen arvo riippuukappaleen nopeus kaasussa.
Vahvoja esimerkkejä kaasuista ovat ilma, kotien lämmitykseen ja ruoanlaittoon käytettävä maakaasu, inertit kaasut (Ne, Ar), joita käytetään mainonnan hehkuputkien täyttämiseen tai joita käytetään luomaan inertti (ei-aggressiivinen, suojaava) ympäristö hitsauksen aikana.
Ihanteellinen kaasu
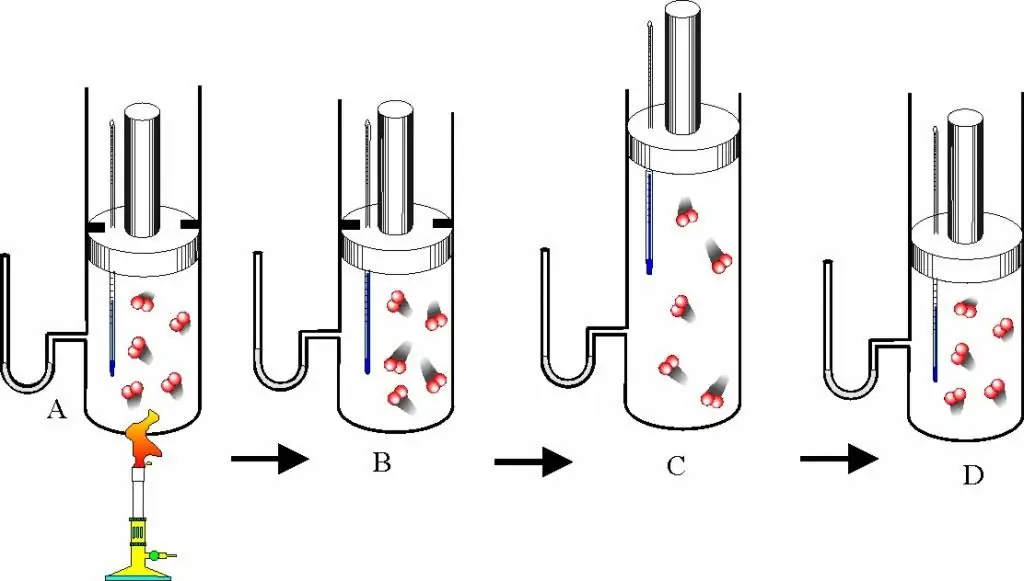
Ennen kuin ryhdyt kuvaamaan kaasulakeja ja tilayhtälöä, sinun tulee ymmärtää hyvin kysymys siitä, mikä on ihanteellinen kaasu. Tämä käsite on otettu käyttöön molekyylikineettisessä teoriassa (MKT). Ihanteellinen kaasu on mikä tahansa kaasu, joka täyttää seuraavat ominaisuudet:
- Sen muodostavat hiukkaset eivät ole vuorovaikutuksessa toistensa kanssa paitsi suorissa mekaanisissa törmäyksissä.
- Jos hiukkaset törmäävät aluksen seiniin tai keskenään, niiden liike-energia ja liikemäärä säilyvät, eli törmäystä pidetään ehdottoman elastisena.
- Partikkeleilla ei ole mittoja, mutta niillä on äärellinen massa, eli ne ovat samanlaisia kuin materiaalipisteet.
On luonnollista, että mikä tahansa kaasu ei ole ihanteellinen, vaan todellinen. Kuitenkin monien käytännön ongelmien ratkaisemiseksi nämä likiarvot ovat varsin päteviä ja niitä voidaan käyttää. On olemassa yleinen empiirinen sääntö, joka sanoo: kemiallisesta luonteesta riippumatta, jos kaasun lämpötila on huoneenlämpötilaa korkeampi ja paine on suuruusluokkaa ilmakehän tai sitä alhaisempi, niin sitä voidaan pitää ihanteellisena suurella tarkkuudella ja sitä voidaan käyttää kuvaamaan se.ideaalisen kaasun tilayhtälön kaava.
Clapeyron-Mendelejevin laki
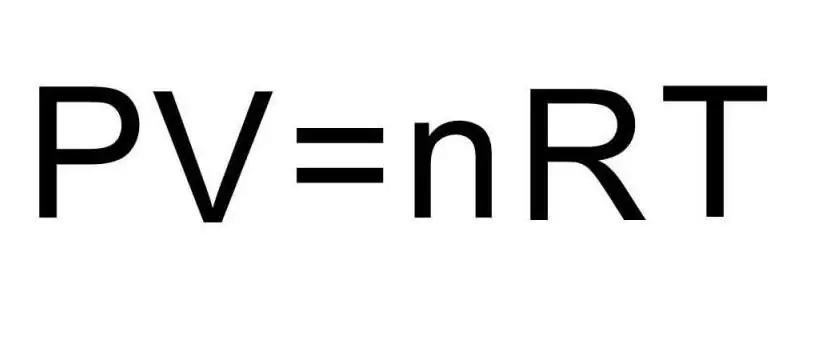
Siirtymät aineen eri aggregaattitilojen ja prosessien välillä yhdessä aggregaattitilassa käsitellään termodynamiikassa. Paine, lämpötila ja tilavuus ovat kolme suuretta, jotka määrittelevät yksiselitteisesti minkä tahansa termodynaamisen järjestelmän tilan. Ihanteellisen kaasun tilayhtälön kaava yhdistää kaikki nämä kolme suuretta yhdeksi yhtälöksi. Kirjoitetaan tämä kaava:
PV=nRT
Tässä P, V, T - paine, tilavuus, lämpötila, vastaavasti. Arvo n on aineen määrä mooleina ja symboli R tarkoittaa kaasujen yleisvakiota. Tämä yhtälö osoittaa, että mitä suurempi paineen ja tilavuuden tulo, sitä suurempi tulee olla aineen määrän ja lämpötilan tulo.

Kaasun tilayhtälön kaavaa kutsutaan Clapeyron-Mendeleevin laiksi. Vuonna 1834 ranskalainen tiedemies Emile Clapeyron, joka tiivisti edeltäjiensä kokeelliset tulokset, päätyi tähän yhtälöön. Clapeyron käytti kuitenkin useita vakioita, jotka Mendelejev korvasi myöhemmin yhdellä - yleisellä kaasuvakiolla R (8, 314 J / (molK)). Siksi nykyfysiikassa tämä yhtälö on nimetty ranskalaisten ja venäläisten tiedemiesten nimien mukaan.

Muut yhtälömuodot
Yllä kirjoitimme Mendeleev-Clapeyronin tilayhtälön ihanteelliselle kaasulle yleisesti hyväksytyssä jakätevä muoto. Termodynamiikan ongelmissa voidaan kuitenkin usein tarvita hieman erilaista muotoa. Alla on kirjoitettu kolme muuta kaavaa, jotka seuraavat suoraan kirjoitetusta yhtälöstä:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Nämä kolme yhtälöä ovat universaaleja myös ihanteelliselle kaasulle, vain niissä esiintyvät suuret kuten massa m, moolimassa M, tiheys ρ ja järjestelmän muodostavien hiukkasten lukumäärä N. Symboli kB tarkoittaa tässä Boltzmannin vakiota (1, 3810-23J/K).
Boyle-Mariotten laki
Kun Clapeyron laati yhtälön, hän perustui kaasulakeihin, jotka oli löydetty kokeellisesti useita vuosikymmeniä aikaisemmin. Yksi niistä on Boyle-Mariotten laki. Se kuvastaa isotermistä prosessia suljetussa järjestelmässä, jonka seurauksena sellaiset makroskooppiset parametrit kuin paine ja tilavuus muuttuvat. Jos laitamme T ja n vakion ihanteellisen kaasun tilayhtälöön, niin kaasulaki on tällöin muodossa:
P1V1=P2V 2
Tämä on Boyle-Mariotten laki, joka sanoo, että paineen ja tilavuuden tulo säilyy mieliv altaisen isotermisen prosessin aikana. Tässä tapauksessa itse arvot P ja V muuttuvat.
Jos kuvaat P(V) tai V(P), isotermit ovat hyperboleja.
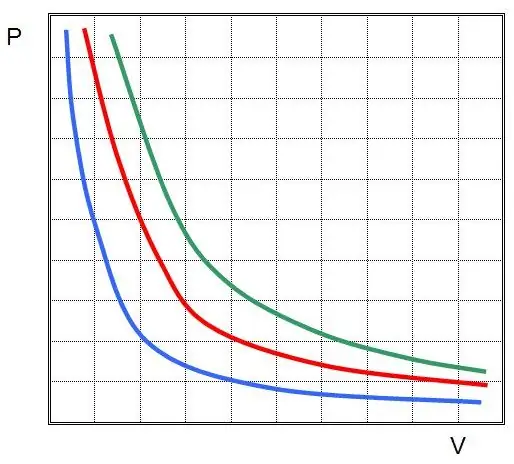
Charlesin ja Gay-Lussacin lait
Nämä lait kuvaavat matemaattisesti isobaarista ja isokoristaprosessit, eli sellaiset siirtymät kaasujärjestelmän tilojen välillä, joissa paine ja tilavuus säilyvät vastaavasti. Charlesin laki voidaan kirjoittaa matemaattisesti seuraavasti:
V/T=vakio, kun n, P=vakio.
Gay-Lussacin laki on kirjoitettu seuraavasti:
P/T=vakio, kun n, V=vakio.
Jos molemmat yhtälöt esitetään graafin muodossa, saadaan suoria viivoja, jotka ovat vinossa jossain kulmassa x-akseliin nähden. Tämän tyyppinen kaavio osoittaa suoran verrannollisuuden tilavuuden ja lämpötilan välillä vakiopaineessa sekä paineen ja lämpötilan välillä vakiotilavuudessa.
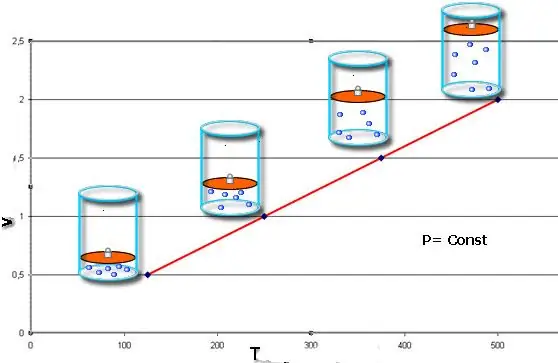
Huomaa, että kaikki kolme tarkasteltua kaasulakia eivät ota huomioon kaasun kemiallista koostumusta eivätkä sen ainemäärän muutosta.
Absoluuttinen lämpötila
Arjessa olemme tottuneet käyttämään Celsius-lämpötila-asteikkoa, sillä se on kätevä kuvaamaan ympärillämme olevia prosesseja. Joten vesi kiehuu 100 oC:ssa ja jäätyy 0 oC:ssa. Fysiikassa tämä asteikko osoittautuu hankalaksi, joten käytetään niin kutsuttua absoluuttista lämpötila-asteikkoa, jonka Lord Kelvin otti käyttöön 1800-luvun puolivälissä. Tämän asteikon mukaisesti lämpötila mitataan kelvineinä (K).
Uskotaan, että lämpötilassa -273, 15 oC atomien ja molekyylien lämpövärähtelyjä ei esiinny, niiden liike eteenpäin pysähtyy kokonaan. Tämä lämpötila Celsius-asteina vastaa absoluuttista nollaa kelvineinä (0 K). Tästä määritelmästäabsoluuttisen lämpötilan fysikaalinen merkitys seuraa: se on aineen muodostavien hiukkasten, esimerkiksi atomien tai molekyylien, kineettisen energian mitta.
Yllä olevan absoluuttisen lämpötilan fyysisen merkityksen lisäksi on olemassa muita tapoja ymmärtää tämä määrä. Yksi niistä on mainittu Charlesin kaasulaki. Kirjoitetaan se seuraavassa muodossa:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Viimeinen yhtälö sanoo, että tietyllä määrällä ainetta järjestelmässä (esimerkiksi 1 mol) ja tietyllä paineella (esimerkiksi 1 Pa) kaasutilavuus määrittää yksiselitteisesti absoluuttisen lämpötilan. Toisin sanoen kaasun tilavuuden kasvu näissä olosuhteissa on mahdollista vain lämpötilan nousun vuoksi, ja tilavuuden pieneneminen osoittaa T.
:n arvon pienenemistä.
Muista, että toisin kuin Celsius-lämpötila, absoluuttinen lämpötila ei voi olla negatiivinen.
Avogadro-periaate ja kaasuseokset
Yllä olevien kaasulakien lisäksi ihanteellisen kaasun tilayhtälö johtaa myös Amedeo Avogadron 1800-luvun alussa löytämään periaatteeseen, joka kantaa hänen sukunimeään. Tämä periaate määrittää, että minkä tahansa kaasun tilavuus vakiopaineessa ja -lämpötilassa määräytyy järjestelmän aineen määrän mukaan. Vastaava kaava näyttää tältä:
n/V=vakio, kun P, T=vakio.
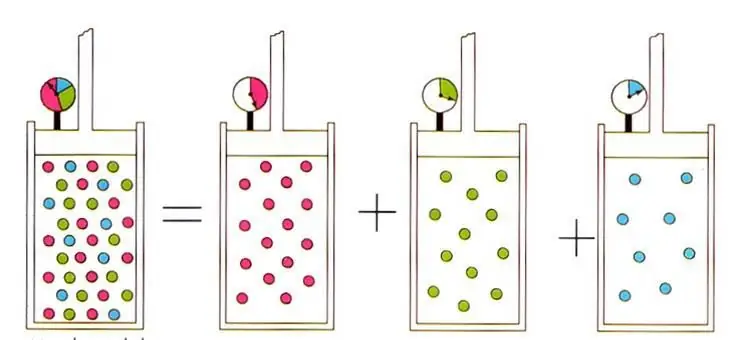
Kirjallinen ilmaus johtaa ideaalikaasufysiikassa hyvin tunnettuun D altonin kaasuseoksia koskevaan lakiin. Tämälain mukaan kaasun osapaine seoksessa määräytyy yksiselitteisesti sen atomiosuuden perusteella.
Esimerkki ongelmanratkaisusta
Suljetussa astiassa, jossa on jäykät seinämät ja joka sisältää ihanteellista kaasua, paine nousi lämmityksen seurauksena 3 kertaa. Järjestelmän lopullinen lämpötila on määritettävä, jos sen alkuarvo oli 25 oC.
Muunnetaan ensin lämpötila Celsius-asteista Kelvineiksi, meillä on:
T=25 + 273, 15=298, 15 K.
Koska astian seinämät ovat jäykkiä, lämmitysprosessia voidaan pitää isokorisena. Tässä tapauksessa noudatamme Gay-Lussac-lakia, meillä on:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Siten lopullinen lämpötila määritetään painesuhteen ja alkulämpötilan tulosta. Korvaamalla tiedot tasa-arvoon, saadaan vastaus: T2=894,45 K. Tämä lämpötila vastaa 621,3 oC.






