MCT-perusyhtälö ja lämpötilan mittaus

2024 Kirjoittaja: Angel Austin | [email protected]. Viimeksi muokattu: 2024-01-15 17:24

Tilastojärjestelmissä tapahtuvien prosessien tutkimista vaikeuttaa hiukkasten pienin koko ja niiden v altava määrä. On käytännössä mahdotonta tarkastella jokaista hiukkasta erikseen, joten otetaan käyttöön tilastolliset suureet: hiukkasten keskinopeus, niiden pitoisuus, hiukkasmassa. Kaavaa, joka kuvaa järjestelmän tilaa mikroskooppiset parametrit huomioiden, kutsutaan kaasujen molekyylikineettisen teorian (MKT) perusyhtälöksi.

Hieman keskimääräisestä hiukkasnopeudesta

Partikkelien nopeuden määrittäminen tehtiin ensin kokeellisesti. Otto Sternin suorittama koulun opetussuunnitelmasta tunnettu kokeilu mahdollisti käsityksen luomisen hiukkasnopeuksista. Kokeen aikana tutkittiin hopeaatomien liikettä pyörivissä sylintereissä: ensin asennuksen paikallaan ollessa, sitten sen pyöriessä tietyllä kulmanopeudella.

Tuloksena havaittiin, että hopeamolekyylien nopeus ylittää äänen nopeuden ja on 500 m/s. Tosiasia on varsin mielenkiintoinen, koska ihmisen on vaikea tuntea tällaisia hiukkasten liikkumisnopeuksia aineissa.

Ihanteellinen kaasu

Jatka tutkimustaSe näyttää mahdolliselta vain järjestelmässä, jonka parametrit voidaan määrittää suorilla mittauksilla fyysisillä instrumenteilla. Nopeutta mitataan nopeusmittarilla, mutta ajatus nopeusmittarin kiinnittämisestä yhteen hiukkaseen on absurdi. Vain hiukkasten liikkeeseen liittyvä makroskooppinen parametri voidaan mitata suoraan.

Harkitse kaasun painetta. Astian seinämiin kohdistuva paine syntyy astiassa olevien kaasumolekyylien vaikutuksista. Aineen kaasumaisen olomuodon erityispiirre on hiukkasten riittävän suuret etäisyydet ja niiden pieni vuorovaikutus keskenään. Näin voit mitata sen paineen suoraan.

Kaikille vuorovaikutuksessa olevien kappaleiden järjestelmälle on ominaista potentiaalienergia ja liike-energia. Todellinen kaasu on monimutkainen järjestelmä. Potentiaalienergian vaihtelu ei sovellu systematisointiin. Ongelma voidaan ratkaista ottamalla käyttöön malli, joka kantaa kaasun tunnusomaiset ominaisuudet syrjään vuorovaikutuksen monimutkaisuuden.

Ideaalikaasu on aineen tila, jossa hiukkasten vuorovaikutus on mitätön, vuorovaikutuksen potentiaalienergia pyrkii olemaan nolla. Vain liikkeen energiaa, joka riippuu hiukkasten nopeudesta, voidaan pitää merkittävänä.

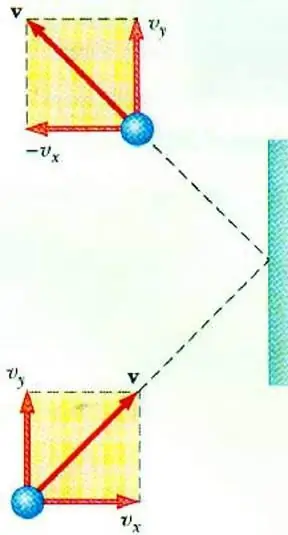
Ihanteellinen kaasunpaine

Kaasun paineen ja sen hiukkasten nopeuden välisen suhteen paljastaminen mahdollistaa ihanteellisen kaasun MKT:n perusyhtälön. Astiassa liikkuva hiukkanen siirtää seinään osuessaan siihen impulssin, jonka arvo voidaan määrittää toisen lain perusteella. Newton:

F∆t=2m₀v_x

Hartikkelin liikemäärän muutos elastisen iskun aikana liittyy sen nopeuden vaakasuuntaisen komponentin muutokseen. F on voima, joka vaikuttaa hiukkasen sivulta seinään lyhyen ajan t; m₀ – hiukkasmassa.

Kaikki kaasuhiukkaset törmäävät alueen S pintaan ajan ∆t aikana liikkuen pinnan suuntaan nopeudella v_x ja sijaitsevat sylinterissä, jonka tilavuus on Sυ _{x Δt. Partikkelipitoisuudella n tasan puolet molekyyleistä liikkuu seinää kohti, toinen puoli liikkuu vastakkaiseen suuntaan.}

Otettuaan huomioon kaikkien hiukkasten törmäyksen, voimme kirjoittaa Newtonin lain alueelle vaikuttavalle voimalle:

F∆t=nm₀v_x²S∆t

Koska kaasun paine määritellään pintaan kohtisuoraan vaikuttavan voiman suhteeksi pinta-alaan, voimme kirjoittaa:

p=F: S=nm₀v_x²

Tuloksena oleva relaatio MKT:n perusyhtälönä ei voi kuvata koko järjestelmää, koska huomioidaan vain yksi liikesuunta.

Maxwell-jakelu

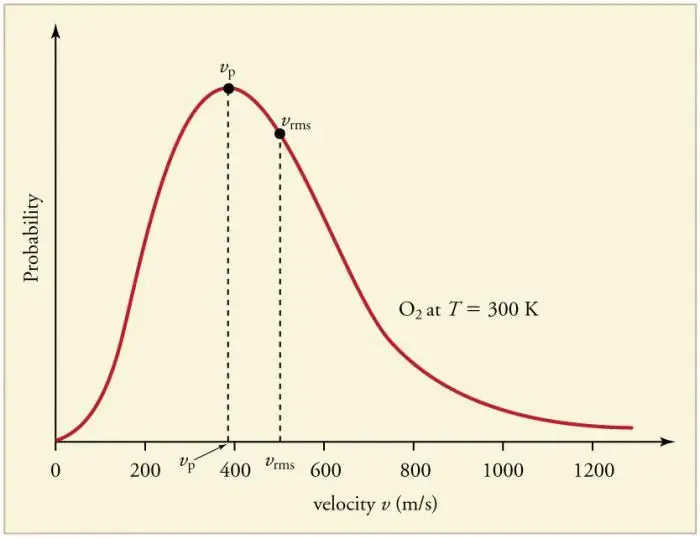
Kaasuhiukkasten jatkuvat toistuvat törmäykset seiniin ja toisiinsa johtavat hiukkasten tietyn tilastollisen jakauman muodostumiseen nopeuksilla (energioilla). Kaikkien nopeusvektorien suunnat osoittautuvat yhtä todennäköisiksi. Tätä jakaumaa kutsutaan Maxwell-jakaumaksi. Vuonna 1860 tämä malli olijohdettu J. Maxwell MKT:n perusteella. Jakaumalain pääparametreja kutsutaan nopeuksiksi: todennäköinen, joka vastaa käyrän maksimiarvoa, ja neliöjuuriarvo v_kv=√‹v² › - hiukkasnopeuden keskineliö.

Kaasun lämpötilan nousu vastaa nopeuden nousua.

Perustuen siihen tosiasiaan, että kaikki nopeudet ovat samat ja niiden moduuleilla on sama arvo, voimme olettaa:

‹v²›=‹v_x²› + ‹v y2^{› + ‹v}z2^{›, alkaen: ‹ v}x2^›=‹v2^{›: 3}

MKT:n perusyhtälö, ottaen huomioon kaasunpaineen keskiarvon, on:

p=nm₀‹v²›: 3.

Tämä suhde on ainutlaatuinen siinä mielessä, että se määrittää suhteen mikroskooppisten parametrien välillä: nopeus, hiukkasmassa, hiukkaspitoisuus ja kaasun paine yleensä.

Käyttäen hiukkasten liike-energian käsitettä MKT:n perusyhtälö voidaan kirjoittaa eri tavalla:

p=2nm₀‹v²›: 6=2n‹E_k›: 3

Kaasun paine on verrannollinen sen hiukkasten kineettisen energian keskiarvoon.

Lämpötila

Mielenkiintoista on, että vakiomäärälle kaasua suljetussa astiassa voidaan suhteuttaa kaasun paine ja hiukkasten liikeenergian keskiarvo. Tässä tapauksessa painetta voidaan mitata mittaamalla energiaahiukkasia.

Mitä tehdä? Mitä arvoa voidaan verrata kineettiseen energiaan? Lämpötila osoittautuu sellaiseksi arvoksi.

Lämpötila on aineiden lämpötilan mitta. Sen mittaamiseen käytetään lämpömittaria, jonka perustana on käyttönesteen (alkoholi, elohopea) lämpölaajeneminen kuumennettaessa. Lämpömittarin asteikko luodaan kokeellisesti. Yleensä siihen sijoitetaan merkkejä, jotka vastaavat työnesteen asentoa jonkin jatkuvassa lämpötilassa tapahtuvan fysikaalisen prosessin aikana (kiehuva vesi, sulava jää). Eri lämpömittareissa on eri asteikot. Esimerkiksi Celsius, Fahrenheit.

Yleinen lämpötila-asteikko

Kaasulämpömittareita voidaan pitää mielenkiintoisempana riippumattomuuden kann alta käyttönesteen ominaisuuksista. Niiden asteikko ei riipu käytetyn kaasun tyypistä. Tällaisessa laitteessa voidaan hypoteettisesti erottaa lämpötila, jossa kaasun paine pyrkii nollaan. Laskelmat osoittavat, että tämä arvo vastaa -273.15 ^oC. Lämpötila-asteikko (absoluuttinen lämpötila-asteikko tai Kelvin-asteikko) otettiin käyttöön vuonna 1848. Tämän asteikon pääpisteeksi otettiin mahdollinen nollakaasun paineen lämpötila. Asteikon yksikkösegmentti on yhtä suuri kuin Celsius-asteikon yksikköarvo. Vaikuttaa kätevämmältä kirjoittaa MKT-perusyhtälö muistiin lämpötilan avulla, kun tutkitaan kaasuprosesseja.

Paineen ja lämpötilan välinen suhde

Kokeellisesti voit varmistaa senkaasun paineen suhteellisuus sen lämpötilaan. Samalla havaittiin, että paine on suoraan verrannollinen hiukkasten pitoisuuteen:

P=nkT,

jossa T on absoluuttinen lämpötila, k on vakio, joka on yhtä suuri kuin 1,38•10^-23J/K.

Perusarvoa, jolla on vakioarvo kaikille kaasuille, kutsutaan Boltzmannin vakioksi.

Vertaamalla paineen riippuvuutta lämpötilasta ja MKT-kaasujen perusyhtälöä, voimme kirjoittaa:

‹E_k›=3kT: 2

Kaasumolekyylien liikkeen kineettisen energian keskiarvo on verrannollinen sen lämpötilaan. Toisin sanoen lämpötila voi toimia hiukkasten liikkeen kineettisen energian mittana.