On esineitä, jotka pystyvät muuttamaan niihin tulevan sähkömagneettisen säteilyvuon tiheyttä, eli joko lisäämään sitä keräämällä sitä yhdessä pisteessä tai vähentämään sitä sirottamalla. Näitä esineitä kutsutaan fysiikassa linsseiksi. Katsotaanpa tätä asiaa tarkemmin.
Mitä ovat linssit fysiikassa?
Tämä käsite tarkoittaa ehdottomasti mitä tahansa esinettä, joka pystyy muuttamaan sähkömagneettisen säteilyn etenemissuuntaa. Tämä on linssien yleinen määritelmä fysiikassa, joka sisältää optiset lasit, magneettiset ja gravitaatiolinssit.
Tässä artikkelissa keskitytään optisiin laseihin, jotka ovat läpinäkyvästä materiaalista valmistettuja esineitä, joita rajoittaa kaksi pintaa. Yhdellä näistä pinnoista on välttämättä oltava kaarevuus (eli sen on oltava osa rajallisen säteen palloa), muuten esineellä ei ole ominaisuutta muuttaa valonsäteiden etenemissuuntaa.
Linssin periaate

Tämän mutkattoman työn ydinoptinen esine on auringonsäteiden taittuman ilmiö. 1600-luvun alussa kuuluisa hollantilainen fyysikko ja tähtitieteilijä Willebrord Snell van Rooyen julkaisi taittumislain, joka tällä hetkellä kantaa hänen sukunimeään. Tämän lain muoto on seuraava: kun auringonvalo kulkee kahden optisesti läpinäkyvän aineen välisen rajapinnan läpi, saadaan säteen ja pinnan normaalin välisen tulokulman sinin ja väliaineen taitekertoimen tulo, jossa se leviää on vakioarvo.

Edellisen selventämiseksi annetaan esimerkki: anna valon pudota veden pinnalle, kun taas pinnan normaalin ja säteen välinen kulma on θ1. Sitten valonsäde taittuu ja alkaa etenemään vedessä jo kulmassa θ2 pinnan normaaliin nähden. Snellin lain mukaan saamme: sin(θ1)n1=synti(θ2) n2, jossa n1 ja n2 ovat ilman ja veden taitekertoimia, vastaavasti. Mikä on taitekerroin? Tämä on arvo, joka osoittaa kuinka monta kertaa sähkömagneettisten a altojen etenemisnopeus tyhjiössä on suurempi kuin optisesti läpinäkyvän väliaineen, eli n=c/v, missä c ja v ovat valon nopeudet tyhjiössä ja keskikokoinen.
Taittumisen ilmentymisen fysiikka piilee Fermatin periaatteen toteuttamisessa, jonka mukaan valo liikkuu siten, että se ylittää etäisyyden pisteestä toiseen avaruudessa lyhimmässä ajassa.
Linssityypit

Optisten linssien tyyppi fysiikassa määräytyy yksinomaan sen muodostavien pintojen muodon perusteella. Niihin tulevan säteen taittumissuunta riippuu tästä muodosta. Joten, jos pinnan kaarevuus on positiivinen (kupera), niin linssistä poistuessaan valonsäde etenee lähemmäs optista akseliaan (katso alla). Toisa alta, jos pinnan kaarevuus on negatiivinen (kovera), optisen lasin läpi kulkeva säde siirtyy pois keskiakselistaan.
Huomaa jälleen, että minkä tahansa kaarevuuden omaava pinta taittaa säteet samalla tavalla (Stellan lain mukaan), mutta niiden normaalien k altevuus optiseen akseliin nähden on erilainen, mikä johtaa taittuneen säteen erilaiseen käyttäytymiseen.
Kahden kuperan pinnan rajaamaa linssiä kutsutaan suppenevaksi linssiksi. Jos se puolestaan muodostuu kahdesta pinnasta, joilla on negatiivinen kaarevuus, sitä kutsutaan sironnaksi. Kaikki muut optiset lasit yhdistetään näiden pintojen yhdistelmään, johon on myös lisätty taso. Yhdistetyn linssin ominaisuus (divergentti tai suppeneva) riippuu sen pintojen säteiden kokonaiskaarevuudesta.
Linssielementit ja säteen ominaisuudet

Jos haluat rakentaa linssejä kuvafysiikkaan, sinun on tutustuttava tämän objektin elementteihin. Ne on lueteltu alla:
- Optinen pääakseli ja keskus. Ensimmäisessä tapauksessa ne tarkoittavat suoraa linjaa, joka kulkee kohtisuorassa linssiin nähden sen optisen keskipisteen läpi. Jälkimmäinen puolestaan on linssin sisällä oleva piste, jonka läpi säde ei taitu.
- Polttoväli ja tarkennus - etäisyys keskustan ja optisen akselin pisteen välillä, joka kerää kaikki linssiin tämän akselin suuntaisesti tulevat säteet. Tämä määritelmä pätee optisten lasien keräämiseen. Divergenttien linssien tapauksessa säteet eivät itse lähenty pisteeseen, vaan niiden kuvitteellinen jatkumo. Tätä pistettä kutsutaan pääpainopisteeksi.
- Optinen teho. Tämä on polttovälin käänteisluvun nimi, eli D \u003d 1 / f. Se mitataan dioptria (dioptria), eli 1 dioptria.=1 m-1.
Seuraavat ovat linssin läpi kulkevien säteiden pääominaisuudet:
- optisen keskuksen läpi kulkeva säde ei muuta liikesuuntaansa;
- optisen pääakselin suuntaisesti tulevat säteet muuttavat suuntaaan siten, että ne kulkevat pääfokustuksen läpi;
- optiselle lasille missä tahansa kulmassa putoavat, mutta sen fokuksen läpi kulkevat säteet muuttavat etenemissuuntaansa siten, että niistä tulee yhdensuuntaisia optisen pääakselin kanssa.
Yllä olevia säteiden ominaisuuksia ohuille linsseille fysiikassa (niin niitä kutsutaan, koska riippumatta siitä, mitä palloja ne muodostuvat ja kuinka paksut ne ovat, vain kohteen optisilla ominaisuuksilla on väliä) käytetään kuvien rakentamiseen niihin..
Kuvat optisissa laseissa: kuinka rakentaa?
Alla on kuva, joka esittää yksityiskohtaisesti kaavioita kuvien rakentamiseksi kohteen kuperaan ja koveraan linssiin(punainen nuoli) riippuen sen sijainnista.
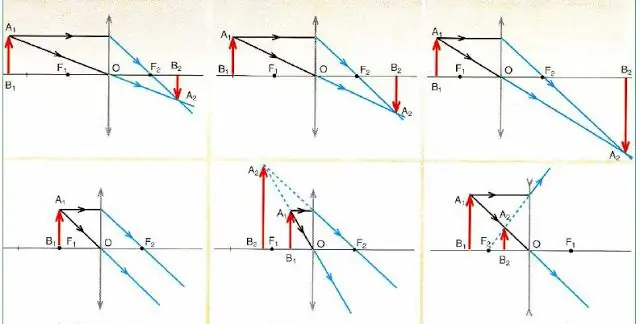
Kuvan piirien analyysistä seuraa tärkeitä johtopäätöksiä:
- Mikä tahansa kuva rakentuu vain kahdelle säteelle (joka kulkee keskustan läpi ja yhdensuuntainen optisen pääakselin kanssa).
- Suuntuvat linssit (merkitty nuolilla päissä ulospäin) voivat antaa sekä suurennetun että pienennetyn kuvan, joka puolestaan voi olla todellinen (tosi) tai kuvitteellinen.
- Jos kohde on tarkennettu, linssi ei muodosta kuvaansa (katso alempi kaavio kuvassa vasemmalla).
- Hajoavat optiset lasit (merkitty sisäänpäin osoittavilla nuolilla) antavat aina pienennetyn ja virtuaalisen kuvan riippumatta kohteen sijainnista.
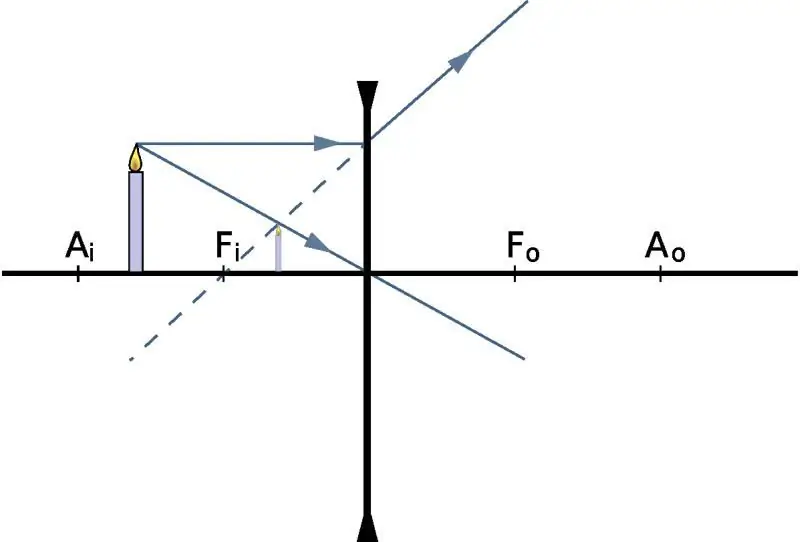
Etäisyyden löytäminen kuvaan
Jotta määritetään, millä etäisyydellä kuva näkyy, ja tiedämme itse kohteen sijainnin, annamme fysiikan linssin kaavan: 1/f=1/do + 1 /d i, jossa do ja di ovat etäisyys kohteeseen ja sen kuvaan optisesta keskus, vastaavasti, f on pääpaino. Jos puhumme keräävästä optisesta lasista, f-luku on positiivinen. Kääntäen, divergenttiobjektiivilla f on negatiivinen.
Käytetään tätä kaavaa ja ratkaistaan yksinkertainen tehtävä: olkoon kohteen etäisyydellä do=2f keräävän optisen lasin keskustasta. Missä hänen kuvansa tulee näkyviin?
Ongelman ehdosta saamme: 1/f=1/(2f)+1/di. Alkaen: 1/di=1/f - 1/(2f)=1/(2f), eli di=2 f. Siten kuva näkyy kahden polttopisteen etäisyydellä linssistä, mutta toiselle puolelle kuin itse kohde (tämän ilmaisee arvon di positiivinen etumerkki).
Lyhyt historia
On mielenkiintoista kertoa sanan "linssi" etymologia. Se tulee latinan sanoista lens ja lentis, mikä tarkoittaa "linssiä", koska optiset esineet näyttävät muodoltaan todella tämän kasvin hedelmiltä.
Muinaiset roomalaiset tunsivat pallomaisten läpinäkyvien kappaleiden taittovoiman. Tätä tarkoitusta varten he käyttivät pyöreitä lasiastioita, jotka oli täytetty vedellä. Itse lasilinssejä alettiin valmistaa Euroopassa vasta 1200-luvulla. Niitä käytettiin lukuvälineenä (modernit lasit tai suurennuslasi).
Optisten esineiden aktiivinen käyttö teleskooppien ja mikroskooppien valmistuksessa juontaa juurensa 1600-luvulle (tämän vuosisadan alussa Galileo keksi ensimmäisen kaukoputken). Huomaa, että hollantilainen tiedemies julkaisi saman 1600-luvun alussa Stellan taittumislain matemaattisen muotoilun, jonka tietämättä on mahdotonta valmistaa linssejä, joilla on halutut ominaisuudet.
Muut linssit
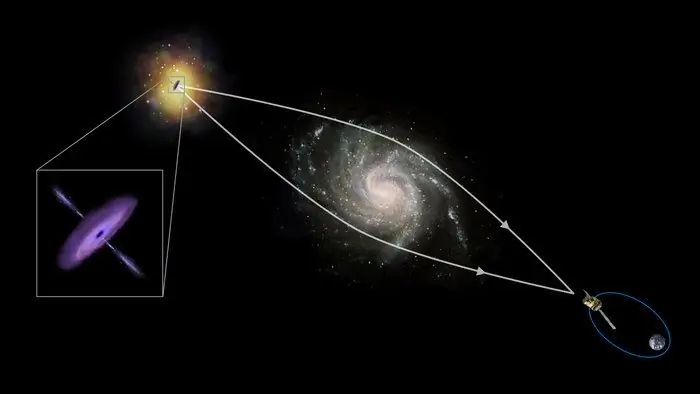
Kuten edellä mainittiin, optisten taitettavien kohteiden lisäksi on olemassa myös magneettisia ja gravitaatiokohteita. Esimerkki edellisistä ovat magneettilinssit elektronimikroskoopissa, elävä esimerkki jälkimmäisestä on valovirran suunnan vääristyminen,kun se kulkee massiivisten avaruuskappaleiden (tähdet, planeetat) läheltä.






