Tärkeä termodynamiikan osa on aineen eri vaiheiden välisten muunnosten tutkiminen, koska näitä prosesseja tapahtuu käytännössä ja niillä on perustavanlaatuinen merkitys järjestelmän käyttäytymisen ennustamisessa tietyissä olosuhteissa. Näitä muunnoksia kutsutaan vaihesiirtymiksi, joille artikkeli on omistettu.
Vaiheen ja järjestelmäkomponentin käsite

Ennen kuin lähdetään tarkastelemaan fysiikan vaihemuutoksia, on tarpeen määritellä itse vaiheen käsite. Kuten yleisen fysiikan kurssista tiedetään, aineella on kolme tilaa: kaasumainen, kiinteä ja nestemäinen. Tieteen erityisosassa - termodynamiikassa - lait on muotoiltu aineen vaiheille, ei niiden aggregaatiotiloille. Faasilla tarkoitetaan tiettyä aineen tilavuutta, jolla on homogeeninen rakenne, jolla on erityiset fysikaaliset ja kemialliset ominaisuudet ja joka on erotettu muusta aineesta rajoilla, joita kutsutaan interfaasiksi.
Siten "vaiheen" käsite sisältää paljon käytännönläheisempää tietoa ominaisuuksistaasia kuin sen aggregaatiotila. Esimerkiksi metallin, kuten raudan kiinteä tila voi olla seuraavissa vaiheissa: matalan lämpötilan magneettinen kappalekeskeinen kuutio (BCC), matalan lämpötilan ei-magneettinen bcc, kasvokeskeinen kuutio (fcc) ja korkea- lämpötila ei-magneettinen bcc.
Vaihekäsitteen lisäksi termodynamiikan laeissa käytetään myös termiä "komponentit", joka tarkoittaa tietyn järjestelmän muodostavien kemiallisten alkuaineiden määrää. Tämä tarkoittaa, että faasi voi olla joko yksikomponenttinen (1 kemiallinen alkuaine) tai monikomponenttinen (useita kemiallisia alkuaineita).
Gibbsin lause ja tasapaino järjestelmän vaiheiden välillä

Vaihemuutosten ymmärtämiseksi on tarpeen tietää niiden väliset tasapainoolosuhteet. Nämä ehdot voidaan saada matemaattisesti ratkaisemalla Gibbsin yhtälöjärjestelmä jokaiselle niistä olettaen, että tasapainotila saavutetaan, kun ulkoisista vaikutuksista eristetyn järjestelmän Gibbsin kokonaisenergia lakkaa muuttumasta.
Esitetyn yhtälöjärjestelmän ratkaisemisen tuloksena saadaan olosuhteet tasapainon olemassaololle useiden vaiheiden välillä: eristetty järjestelmä lakkaa kehittymästä vasta, kun paineet, kunkin komponentin kemialliset potentiaalit ja lämpötilat kaikissa vaiheissa ovat samanarvoisia keskenään.
Gibbsin vaihesääntö tasapainolle

Useista vaiheista ja komponenteista koostuva järjestelmä voi olla tasapainossa paitsitietyissä olosuhteissa, esimerkiksi tietyssä lämpötilassa ja paineessa. Joitakin tasapainon Gibbsin lauseen muuttujia voidaan muuttaa säilyttäen samalla sekä vaiheiden että tässä tasapainossa olevien komponenttien lukumäärän. Muuttujien määrää, joita voidaan muuttaa häiritsemättä järjestelmän tasapainoa, kutsutaan tämän järjestelmän vapauksien lukumääräksi.
F vaiheesta ja k komponentista koostuvan järjestelmän vapauksien lukumäärä l määräytyy yksiselitteisesti Gibbsin vaihesäännöstä. Tämä sääntö on kirjoitettu matemaattisesti seuraavasti: l + f=k + 2. Kuinka työskennellä tämän säännön kanssa? Erittäin yksinkertainen. Esimerkiksi tiedetään, että systeemi koostuu f=3 tasapainofaasista. Kuinka monta komponenttia tällainen järjestelmä voi sisältää? Voit vastata kysymykseen perustelemalla seuraavasti: tasapainon tapauksessa tiukimmat olosuhteet ovat olemassa, kun se toteutuu vain tietyillä indikaattoreilla, eli minkä tahansa termodynaamisen parametrin muutos johtaa epätasapainoon. Tämä tarkoittaa, että vapauksien lukumäärä l=0. Korvaamalla tunnetut l:n ja f:n arvot saadaan k=1, eli järjestelmä, jossa kolme faasia ovat tasapainossa, voi koostua yhdestä komponentista. Hyvä esimerkki on veden kolmoispiste, jossa jää, nestemäinen vesi ja höyry ovat tasapainossa tietyissä lämpötiloissa ja paineissa.
Vaihemuunnosten luokitus
Jos alat muuttaa joitain termodynaamisia parametreja tasapainossa olevassa järjestelmässä, voit tarkkailla, kuinka yksi vaihe katoaa ja toinen ilmaantuu. Yksinkertainen esimerkki tästä prosessista on jään sulaminen sitä kuumennettaessa.
Koska Gibbsin yhtälö riippuu vain kahdesta muuttujasta (paine ja lämpötila) ja faasisiirtymä sisältää muutoksen näissä muuttujissa, niin matemaattisesti vaiheiden välinen siirtymä voidaan kuvata eriyttämällä Gibbsin energia sen suhteen. muuttujia. Tätä lähestymistapaa käytti itäv altalainen fyysikko Paul Ehrenfest vuonna 1933, kun hän laati luokituksen kaikista tunnetuista termodynaamisista prosesseista, jotka tapahtuvat faasitasapainon muuttuessa.
Termodynamiikan perusteista seuraa, että Gibbsin energian ensimmäinen derivaatta lämpötilan suhteen on yhtä suuri kuin muutos järjestelmän entropiassa. Gibbsin energian derivaatta paineen suhteen on yhtä suuri kuin tilavuuden muutos. Jos järjestelmän vaiheiden vaihtuessa entropia tai tilavuus katkeaa, eli ne muuttuvat äkillisesti, niin ne puhuvat ensimmäisen asteen vaihemuutoksesta.
Lisäksi Gibbsin energian toiset derivaatat lämpötilan ja paineen suhteen ovat lämpökapasiteetti ja tilavuuslaajenemiskerroin, vastaavasti. Jos vaiheiden väliseen muutokseen liittyy epäjatkuvuus ilmoitettujen fysikaalisten suureiden arvoissa, puhutaan toisen asteen vaihesiirrosta.
Esimerkkejä vaiheiden välisistä muunnoksista

Luontossa on v altava määrä erilaisia siirtymiä. Tämän luokituksen puitteissa silmiinpistäviä esimerkkejä ensimmäisen tyypin siirtymistä ovat metallien sulamisprosessit tai vesihöyryn kondensoituminen ilmasta, kun järjestelmässä tapahtuu tilavuushyppy.
Jos puhumme toisen asteen siirtymistä, niin silmiinpistäviä esimerkkejä ovat raudan muuttuminen magneettisesta tilasta paramagneettiseen lämpötilassa768 ºC tai metallisen johtimen muuttaminen suprajohtavaan tilaan lämpötiloissa, jotka ovat lähellä absoluuttista nollaa.
Yhtälöt, jotka kuvaavat ensimmäisen tyyppisiä siirtymiä
Käytännössä on usein tarpeen tietää, miten lämpötila, paine ja absorboitunut (vapautettu) energia muuttuvat järjestelmässä, kun siinä tapahtuu vaihemuutoksia. Tätä tarkoitusta varten käytetään kahta tärkeää yhtälöä. Ne on saatu termodynamiikan perusteiden tietämyksen perusteella:
- Clapeyronin kaava, joka määrittää paineen ja lämpötilan välisen suhteen eri faasien välisten muunnosten aikana.
- Clausius-kaava, joka yhdistää absorboidun (vapautetun) energian ja järjestelmän lämpötilan transformaation aikana.
Molempia yhtälöitä ei käytetä vain fysikaalisten suureiden kvantitatiivisten riippuvuuksien saamiseksi, vaan myös tasapainokäyrien k altevuuden merkin määrittämiseen vaihekaavioissa.
Yhtälö toisen tyyppisten siirtymien kuvaamiseen

Ensimmäisen ja toisen tyypin vaihesiirtymiä kuvataan eri yhtälöillä, koska Clausius- ja Clausius-yhtälöiden soveltaminen toisen asteen siirtymisiin johtaa matemaattiseen epävarmuuteen.
Jälkimmäisen kuvaamiseen käytetään Ehrenfest-yhtälöitä, jotka määrittävät paineen ja lämpötilan muutosten välisen suhteen tiedon lämpökapasiteetin ja tilavuuslaajenemiskertoimen muutoksista muunnosprosessin aikana. Ehrenfest-yhtälöitä käytetään kuvaamaan johdin-suprajohteen siirtymiä magneettikentän puuttuessa.
Tärkeäävaihekaaviot
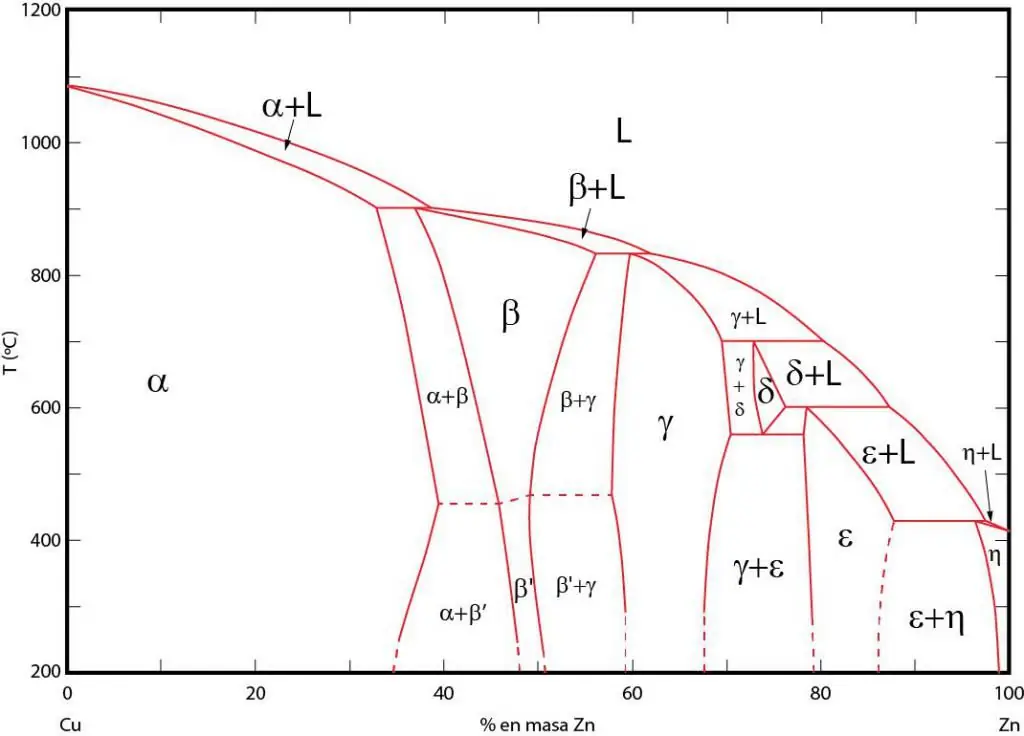
Vaihekaaviot ovat graafinen esitys alueista, joilla vastaavat vaiheet ovat tasapainossa. Nämä alueet erotetaan faasien välisillä tasapainoviivoilla. P-T (paine-lämpötila), T-V (lämpötila-tilavuus) ja P-V (paine-tilavuus) -vaihekaavioita käytetään usein.
Vaihekaavioiden merkitys on siinä, että niiden avulla voit ennustaa, missä vaiheessa järjestelmä on, kun ulkoiset olosuhteet muuttuvat vastaavasti. Tätä tietoa käytetään erilaisten materiaalien lämpökäsittelyssä halutun rakenteen aikaansaamiseksi.






