Ohmin laki on sähköpiirien peruslaki. Samalla se antaa meille mahdollisuuden selittää monia luonnonilmiöitä. Voidaan esimerkiksi ymmärtää, miksi sähkö ei "voita" lintuja, jotka istuvat johtojen päällä. Fysiikassa Ohmin laki on erittäin tärkeä. Ilman hänen tietämystään olisi mahdotonta luoda vakaita sähköpiirejä tai elektroniikkaa ei olisi ollenkaan.
Riippuvuus I=I(U) ja sen arvo
Materiaalien resistanssin löytämisen historia liittyy suoraan virta-jännite-ominaisuuteen. Mikä se on? Otetaan piiri, jolla on jatkuva sähkövirta ja tarkastellaan mitä tahansa sen elementtejä: lamppu, kaasuputki, metallijohdin, elektrolyyttipullo jne.
Muutamalla kyseessä olevaan elementtiin syötettyä jännitettä U (kutsutaan usein V:ksi), seuraamme sen läpi kulkevan virran (I) voimakkuuden muutosta. Tämän seurauksena saamme muodon I \u003d I (U) riippuvuuden, jota kutsutaan "elementin jänniteominaispiirteeksi" ja joka on suora osoitus sensähköiset ominaisuudet.
V/A-ominaisuus voi näyttää erilaiselta eri elementtien os alta. Sen yksinkertaisin muoto saadaan ottamalla huomioon metallijohdin, jonka teki Georg Ohm (1789 - 1854).
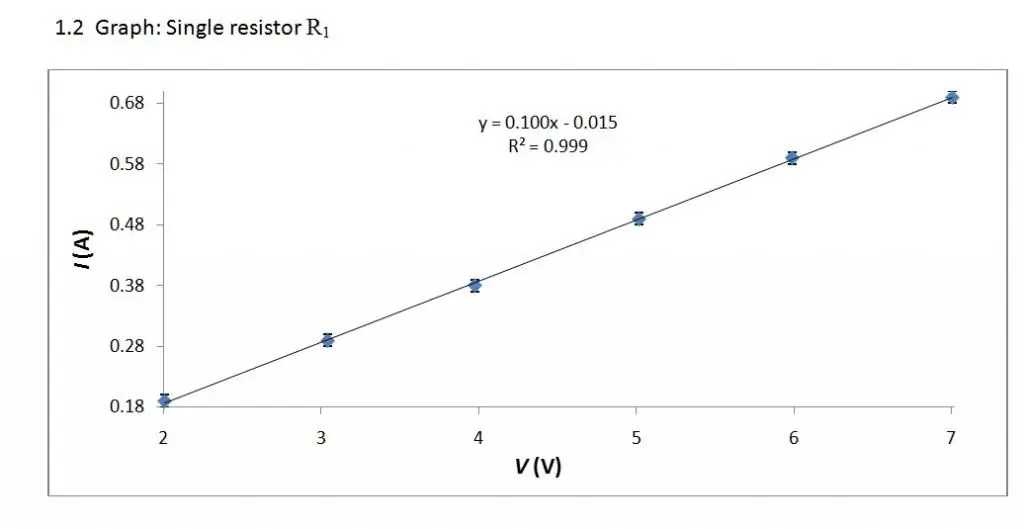
Volttiampeeri-ominaisuus on lineaarinen suhde. Siksi sen kaavio on suora.
Laki yksinkertaisimmassa muodossaan
Ohmin tutkimus johtimien virta-jännite-ominaisuuksista osoitti, että metallijohtimen sisällä oleva virranvoimakkuus on verrannollinen sen päissä olevaan potentiaalieroon (I ~ U) ja kääntäen verrannollinen tiettyyn kertoimeen, eli I ~ 1/R. Tämä kerroin tuli tunnetuksi "johtimen resistanssina", ja sähköisen vastuksen mittayksikkö oli ohm tai V/A.
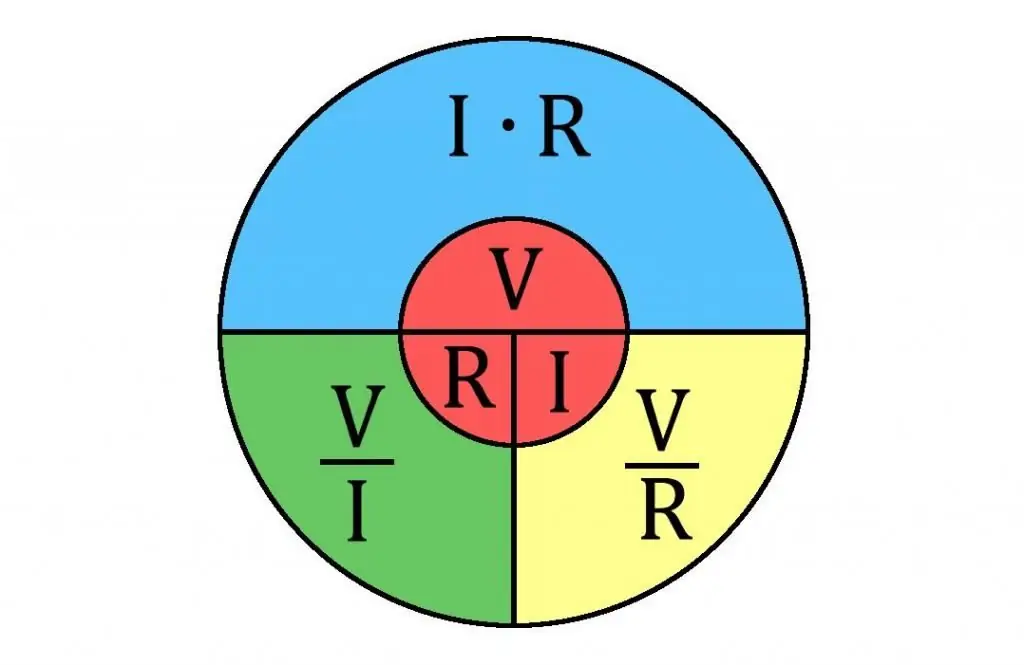
Yksi huomioitava asia. Ohmin lakia käytetään usein resistanssin laskemiseen piireissä.
Lain sanamuoto
Ohmin laki sanoo, että piirin yksittäisen osan virranvoimakkuus (I) on verrannollinen tämän osan jännitteeseen ja kääntäen verrannollinen sen vastukseen.
On huomattava, että tässä muodossa laki pätee vain ketjun homogeeniselle osalle. Homogeeninen on sähköpiirin osa, joka ei sisällä virtalähdettä. Ohmin lain käyttöä epähomogeenisessa piirissä käsitellään alla.
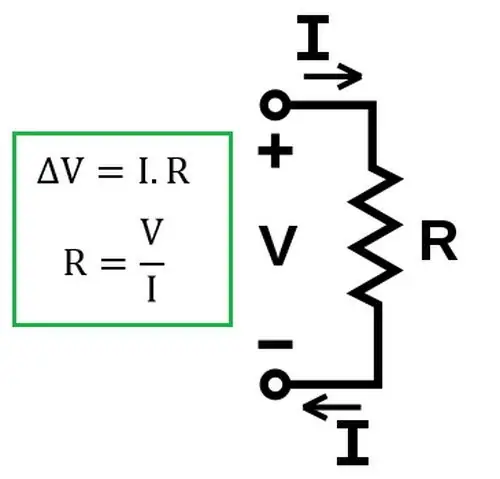
Myöhemmin todettiin kokeellisesti, että laki on edelleen voimassa ratkaisuilleelektrolyytit sähköpiirissä.
Vastuksen fyysinen merkitys
Resistanssi on materiaalien, aineiden tai väliaineiden ominaisuus, joka estää sähkövirran kulkeutumisen. Kvantitatiivisesti 1 ohmin resistanssi tarkoittaa, että johtimessa, jonka päissä on jännite 1 V, voi kulkea 1 A sähkövirta.
Sähkövastus
Kokeellisesti havaittiin, että johtimen sähkövirran vastus riippuu sen mitoista: pituus, leveys, korkeus. Ja myös sen muodosta (pallo, sylinteri) ja materiaali, josta se on valmistettu. Siten esimerkiksi homogeenisen lieriömäisen johtimen resistanssin kaava on: R \u003d pl / S.
Jos tähän kaavaan laitetaan s=1 m2 ja l=1 m, niin R on numeerisesti yhtä suuri kuin p. Tästä lasketaan johtimen ominaisvastuskertoimen mittayksikkö SI:ssä - tämä on Ohmm.

Resistiivisyyskaavassa p on vastuskerroin, joka määräytyy sen materiaalin kemiallisten ominaisuuksien perusteella, joista johdin on valmistettu.
Ohmin lain differentiaalisen muodon huomioon ottamiseksi meidän on harkittava vielä muutamia käsitteitä.
Virtatiheys
Kuten tiedätte, sähkövirta on kaikkien varautuneiden hiukkasten tiukasti määrätty liike. Esimerkiksi metalleissa virran kantajat ovat elektroneja ja johtavissa kaasuissa ioneja.
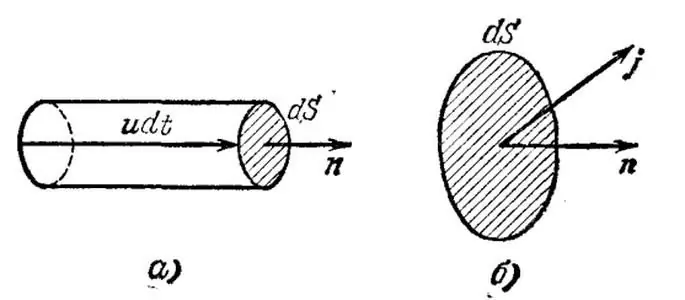
Otetaan triviaali tapaus, kun kaikki nykyiset operaattorithomogeeninen - metallijohdin. Erottakaamme mielessämme äärettömän pieni tilavuus tässä johtimessa ja merkitään u:lla elektronien keskimääräinen (ajautuminen, järjestys) nopeus annetussa tilavuudessa. Lisäksi olkoon n virrankantoa altojen pitoisuus tilavuusyksikköä kohti.
Piirretään nyt äärettömän pieni pinta-ala dS kohtisuoraan vektoriin u ja konstruoidaan nopeuden mukaan äärettömän pieni sylinteri, jonka korkeus on udt, missä dt tarkoittaa aikaa, jonka aikana kaikki tarkasteltavan tilavuuden sisältämät nykyiset nopeudenkantajat kulkevat alueen dS kautta.
Tässä tapauksessa varaus, joka on yhtä suuri kuin q=neudSdt, siirtyy elektronien toimesta alueen läpi, jossa e on elektronin varaus. Siten sähkövirran tiheys on vektori j=neu, joka ilmaisee varauksen määrää, joka siirtyy aikayksikköä kohti pinta-alayksikön läpi.
Yksi Ohmin lain differentiaalimääritelmän eduista on, että pärjäät usein ilman vastuksen laskemista.
Sähkövaraus. Sähkökentän voimakkuus
Kentänvoimakkuus yhdessä sähkövarauksen kanssa on sähköteorian perusparametri. Samalla niistä voidaan saada määrällinen käsitys koululaisten saatavilla olevista yksinkertaisista kokeista.
Yksinkertaisuuden vuoksi harkitsemme sähköstaattista kenttää. Tämä on sähkökenttä, joka ei muutu ajan myötä. Kiinteät sähkövaraukset voivat luoda tällaisen kentän.
Tarvitsemme myös testiveloituksen. Sen kapasiteetissa käytämme varattua runkoa - niin pientä, että se ei pysty aiheuttamaankaikki häiriöt (varausten uudelleenjakauma) ympäröivissä kohteissa.
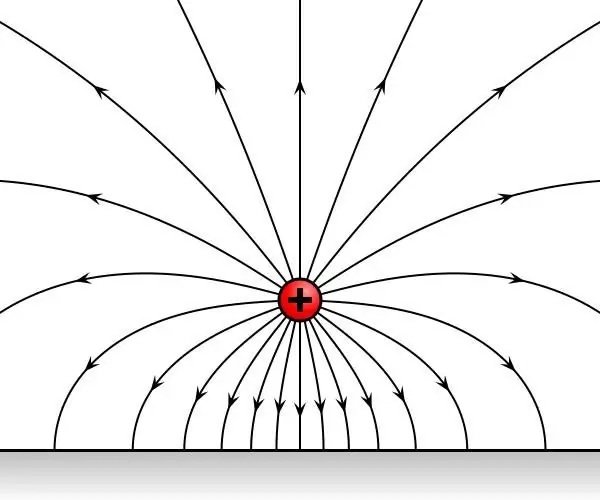
Otellaan vuorollaan kahta otettua testivarausta, jotka on asetettu peräkkäin yhteen pisteeseen avaruudessa, joka on sähköstaattisen kentän vaikutuksen alaisena. Osoittautuu, että syytteet joutuvat hänen puoleltaan ajassa muuttumattomille vaikutuksille. Olkoot F1 ja F2 latauksiin vaikuttavia voimia.
Kokeellisten tietojen yleistyksen tuloksena havaittiin, että voimat F1 ja F2 suuntautuvat joko yhteen tai vastakkaisiin suuntiin, ja niiden suhde F1/F2 on riippumaton avaruuden pisteestä, johon testivaraukset vuorotellen asetettiin. Siksi suhde F1/F2 on ominaisuus itse varauksille, eikä se riipu kentästä.
Tämän tosiasian löytäminen mahdollisti kappaleiden sähköistymisen karakterisoinnin, ja sitä kutsuttiin myöhemmin sähkövaraukseksi. Siten määritelmän mukaan q1/q2=F1/F 2 , jossa q1 ja q2 - kentän yhteen kohtaan asetettujen maksujen määrä ja F 1 ja F2 - voimat, jotka vaikuttavat varauksiin kentän puolelta.
Tällaisten näkökohtien perusteella eri hiukkasten varausten suuruudet määritettiin kokeellisesti. Asettamalla ehdollisesti yksi testimaksuista yhtä suureksi suhteessa yksi, voit laskea toisen varauksen arvon mittaamalla suhteen F1/F2.
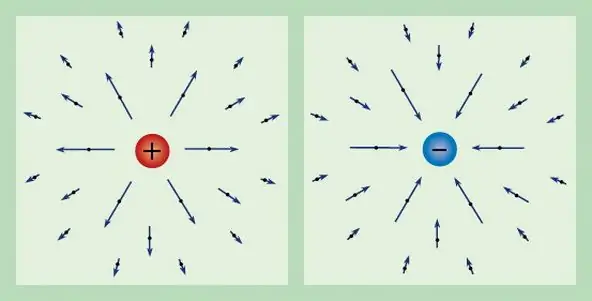
Kaikki sähkökenttä voidaan luonnehtia tunnetulla varauksella. Siten yksikkötestivaraukseen levossa vaikuttavaa voimaa kutsutaan sähkökentän voimakkuudeksi ja sitä merkitään E:llä. Varauksen määritelmästä saadaan, että voimakkuusvektorilla on seuraava muoto: E=F/q.
Vektoreiden j ja E yhteys. Ohmin lain toinen muoto
Homogeenisessa johtimessa varautuneiden hiukkasten järjestynyt liike tapahtuu vektorin E suunnassa. Tämä tarkoittaa, että vektorit j ja E ovat samansuuntaisia. Kuten virrantiheyttä määritettäessä, valitsemme johtimeen äärettömän pienen sylinterimäisen tilavuuden. Sitten virta, joka on yhtä suuri kuin jdS, kulkee tämän sylinterin poikkileikkauksen läpi ja sylinteriin syötetty jännite on yhtä suuri kuin Edl. Sylinterin ominaisvastuskaava tunnetaan myös.
Sitten kirjoittamalla virranvoimakkuuden kaava kahdella tavalla, saadaan: j=E/p, jossa arvoa 1/p kutsutaan sähkönjohtavuudeksi ja se on sähköisen resistiivisyyden käänteisarvo. Sitä merkitään yleensä σ (sigma) tai λ (lambda). Johtavuuden yksikkö on Sm/m, jossa Sm on Siemens. Yksikkö käänteisohm.
Täten voimme vastata yllä esitettyyn kysymykseen Ohmin laista epähomogeeniselle piirille. Tässä tapauksessa sähköstaattisen kentän voima, jolle on tunnusomaista intensiteetti E1, ja muut voimat, jotka vaikuttavat niihin toisesta virtalähteestä, vaikuttavat virrankantoimiin. nimetty E 2. Sitten Ohmin laki soveltuuketjun epähomogeeninen osa näyttää tältä: j=λ(E1 + E2).
Lisätietoja johtavuudesta ja resistanssista
Johtimen kyvylle johtaa sähkövirtaa on tunnusomaista sen ominaisvastus, joka voidaan löytää resistiivisyyskaavan tai johtavuuden avulla, joka lasketaan johtavuuden käänteislukuna. Näiden parametrien arvo määräytyy sekä johdinmateriaalin kemiallisten ominaisuuksien että ulkoisten olosuhteiden mukaan. Erityisesti ympäristön lämpötila.
Useimmille metalleille ominaisvastus normaalilämpötilassa on verrannollinen siihen, eli p ~ T. Alhaisissa lämpötiloissa havaitaan kuitenkin poikkeamia. Useille metalleille ja metalliseoksille lämpötiloissa, jotka ovat lähellä 0°K, vastuslaskelma osoitti nolla-arvoja. Tätä ilmiötä kutsutaan suprajohtavuudeksi. Tämä ominaisuus on esimerkiksi elohopealla, tinalla, lyijyllä, alumiinilla jne. Jokaisella metallilla on oma kriittinen lämpötilansa Tk, jossa havaitaan suprajohtavuus.
Huomaa myös, että sylinterin resistiivisyyden määritelmä voidaan yleistää samasta materiaalista valmistettuihin johtimiin. Tässä tapauksessa poikkileikkausala ominaisvastuskaavasta on yhtä suuri kuin langan poikkileikkaus ja l - sen pituus.






