Eräässä fysiikan - dynamiikan -osiossa, kun he tutkivat kappaleiden liikettä, he ajattelevat liikkuvaan järjestelmään vaikuttavia voimia. Jälkimmäinen voi tehdä sekä positiivista että negatiivista työtä. Mieti tässä artikkelissa, mikä on kitkavoiman työ ja miten se lasketaan.
Työn käsite fysiikassa
Fysiikassa käsite "työ" eroaa tämän sanan tavallisesta ideasta. Työ ymmärretään fyysiseksi suureksi, joka on yhtä suuri kuin voimavektorin ja kappaleen siirtymävektorin skalaaritulo. Oletetaan, että on olemassa jokin esine, johon voima F¯ vaikuttaa. Koska siihen ei vaikuta muita voimia, sen siirtymävektori l¯ osuu suunnassa yhteen vektorin F¯ kanssa. Näiden vektorien skalaaritulo vastaa tässä tapauksessa niiden moduulien tuloa, eli:
A=(F¯l¯)=Fl.
Arvo A on työ, jonka voima F¯ tekee siirtääkseen kohteen etäisyyden l. Kun otetaan huomioon arvojen F ja l mitat, havaitsemme, että työ mitataan newtoneina metriä kohti (Nm) SI-järjestelmässä. Kuitenkin yksikköNm:llä on oma nimi - se on joule. Tämä tarkoittaa, että työn käsite on sama kuin energian käsite. Toisin sanoen, jos 1 newtonin voima siirtää kappaletta 1 metrin, vastaavat energiakustannukset ovat 1 joule.
Mikä on kitkavoima?
Kitkavoiman toimintaa koskevan kysymyksen tutkiminen on mahdollista, jos tiedät minkälaisesta voimasta puhumme. Fysiikassa kitka on prosessi, joka estää yhden kappaleen liikkeen toisen pinnalla, kun nämä pinnat joutuvat kosketuksiin.
Jos tarkastelemme vain kiinteitä kappaleita, niille on olemassa kolmenlaisia kitkaa:
- lepo;
- lipsahdus;
- rullaa.
Nämä voimat vaikuttavat kosketuksissa olevien pintojen väliin ja kohdistuvat aina kappaleiden liikettä vastaan.
Lepokitka estää itse liikkeen, liukukitka ilmenee liikeprosessissa, kun kappaleiden pinnat liukuvat toistensa yli ja pinnalla vierivän kappaleen ja pinnan välillä on vierintäkitka.
Esimerkki staattisen kitkan vaikutuksesta on auto, joka on käsijarrulla rinteessä. Liukukitka ilmenee hiihtäjän liikkuessa lumella tai luistelijan jäällä. Lopuksi vierintäkitka vaikuttaa auton pyörän liikkuessa tiellä.
Kaikkien kolmen kitkatyypin voimat lasketaan seuraavalla kaavalla:
Ft=µtN.
Tässä N on tukireaktiovoima, µt on kitkakerroin. Voima Nosoittaa tuen iskun voimakkuuden runkoon kohtisuorassa pinnan tasoon nähden. Mitä tulee parametriin µt, se mitataan kokeellisesti kullekin hankausmateriaaliparille, esimerkiksi puu-puu, teräs-lumi ja niin edelleen. Mittaustulokset kerätään erityisiin taulukoihin.
Jokaisen kitkavoiman kertoimella µt on oma arvo valitulle materiaaliparille. Näin ollen staattinen kitkakerroin on useita kymmeniä prosentteja suurempi kuin liukukitkan kerroin. Vierintäkerroin puolestaan on 1-2 suuruusluokkaa pienempi kuin liukumisen.
Kitavoimien työ
Nyt, kun olet tutustunut työn käsitteisiin ja kitkan tyyppeihin, voit siirtyä suoraan artikkelin aiheeseen. Tarkastellaan järjestyksessä kaikentyyppisiä kitkavoimia ja selvitetään, mitä työtä ne tekevät.
Aloitetaan staattisesta kitkasta. Tämä tyyppi ilmenee, kun keho ei liiku. Koska liikettä ei ole, sen siirtymävektori l¯ on yhtä suuri kuin nolla. Jälkimmäinen tarkoittaa, että staattisen kitkavoiman työ on myös nolla.
Liukukitka vaikuttaa määritelmän mukaan vain kehon liikkuessa avaruudessa. Koska tämän tyyppisen kitkan voima on aina suunnattu kehon liikettä vastaan, se tarkoittaa, että se tekee negatiivista työtä. A:n arvo voidaan laskea kaavalla:
A=-Ftl=-µtNl.
Liukukitkavoiman työn tarkoituksena on hidastaa kehon liikettä. Tämän työn tuloksena kehon mekaaninen energia muuttuu lämmöksi.

Viirintäkitka, kuten liukuminen, sisältää myös kehon liikkeen. Vierintäkitkavoima tekee negatiivista työtä hidastaen rungon alkukiertoa. Koska puhumme kehon pyörimisestä, on kätevää laskea tämän voiman työn arvo sen liikemäärän työn kautta. Vastaava kaava kirjoitetaan seuraavasti:
A=-Mθ missä M=FtR.
Tässä θ on kappaleen pyörimiskulma pyörimisen seurauksena, R on etäisyys pinnasta pyörimisakseliin (pyörän säde).
Ongelma liukuvan kitkavoiman kanssa
Tiedetään, että puupalikka on vinon puutason reunalla. Taso on vinossa horisonttiin nähden 40o kulmassa. Kun tiedetään, että liukukitkakerroin on 0,4, tason pituus on 1 metri ja tangon massa vastaa 0,5 kg, on tarpeen löytää liukukitka.
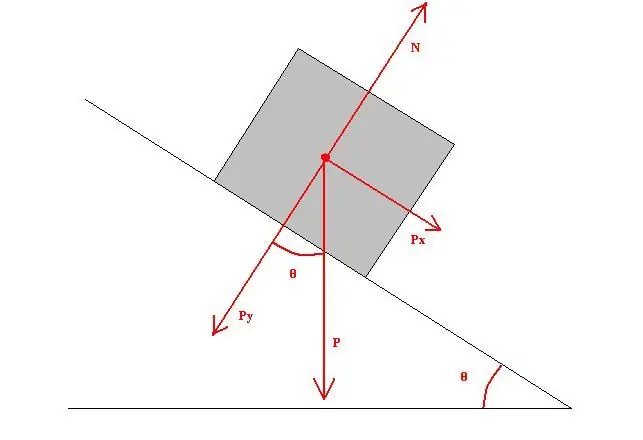
Laske liukukitkavoima. Se on yhtä suuri kuin:
Ft=mgcos(α)µt=0,59,81cos(40 o)0, 4=1,5 N.
Sitten vastaava työ A on:
A=-Ftl=-1,51=-1,5 J.
Viirintäkitkaongelma
Tiedetään, että pyörä vierii tietä pitkin jonkin matkan ja pysähtyi. Pyörän halkaisija on 45 cm Pyörän kierrosten lukumäärä ennen pysähtymistä on 100. Ottaen huomioon vierintäkertoimen 0,03, on selvitettävä, mikä on vierintäkitkavoiman työ. Pyörän massa on 5 kg.

Lasketaan ensin vierintäkitkamomentti:
M=FtR=µtmgD/2=0,0359, 81 0, 45/2=0, 331 Nm.
Jos pyörän tekemien kierrosten määrä kerrotaan 2pi radiaanilla, saadaan pyörän kiertokulma θ. Sitten työn kaava on:
A=-Mθ=-M2pin.
Missä n on kierrosten lukumäärä. Korvaamalla momentin M ja luvun n ehdosta saadaan vaadittu työ: A=- 207.87 J.






