Tämänpäiväisen artikkelimme aiheena on materiaalipisteen kinematiikka. Mistä siinä on kyse? Mitä käsitteitä siinä esiintyy ja mikä määritelmä tälle termille tulisi antaa? Yritämme vastata näihin ja moniin muihin kysymyksiin tänään.
Määritelmä ja käsite
Aineellisen pisteen kinematiikka ei ole muuta kuin fysiikan alaosasto, jota kutsutaan "mekaniikaksi". Hän puolestaan tutkii tiettyjen kappaleiden liikemalleja. Myös materiaalipisteen kinematiikka käsittelee tätä ongelmaa, mutta ei tee sitä yleisesti. Itse asiassa tämä alajakso tutkii menetelmiä, joiden avulla voit kuvata kappaleiden liikkeitä. Tässä tapauksessa vain niin sanotut idealisoidut kappaleet soveltuvat tutkimukseen. Näitä ovat: materiaalipiste, ehdottoman jäykkä runko ja ihanteellinen kaasu. Tarkastellaanpa käsitteitä tarkemmin. Tiedämme kaikki koulun penkistä, että aineelliseksi pisteeksi on tapana kutsua kappaletta, jonka mitat voidaan tietyssä tilanteessa jättää huomiotta. Muuten, materiaalipisteen translaatioliikkeen kinematiikka alkaa ensimmäistä kertaaesiintyy seitsemännen luokan fysiikan oppikirjoissa. Tämä on yksinkertaisin haara, joten on kätevintä aloittaa tutustuminen tieteeseen sen avulla. Erillinen kysymys on, mitkä ovat materiaalipisteen kinematiikan elementit. Niitä on melko paljon, ja ehdollisesti ne voidaan jakaa useille tasoille, joilla on erilainen monimutkaisuus ymmärtämisen vuoksi. Jos puhumme esimerkiksi sädevektorista, sen määrittelyssä ei periaatteessa ole mitään liian monimutkaista. Ymmärrät kuitenkin, että opiskelijan on paljon helpompi ymmärtää se kuin yläkoulun tai lukion opiskelijan. Ja ollakseni rehellinen, tämän termin ominaisuuksia ei tarvitse selittää lukiolaisille.
Kinematiikan luomisen lyhyt historia
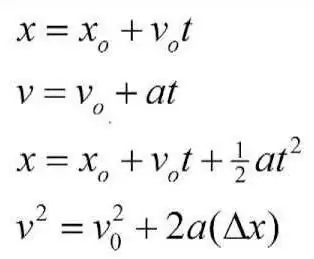
Moni, monta vuotta sitten suuri tiedemies Aristoteles omisti leijonan osan vapaa-ajastaan fysiikan tutkimiseen ja kuvaamiseen erillisenä tieteenä. Hän työskenteli myös kinematiikan parissa yrittäen esittää sen pääteesejä ja käsitteitä tavalla tai toisella, joita käytetään yrityksissä ratkaista käytännön ja jopa arkipäivän ongelmia. Aristoteles antoi alustavat ajatukset siitä, mitkä ovat materiaalipisteen kinematiikan elementit. Hänen työnsä ja teoksensa ovat erittäin arvokkaita koko ihmiskunnalle. Siitä huolimatta hän teki johtopäätöksissään huomattavan määrän virheitä, ja syynä tähän olivat tietyt väärinkäsitykset ja laskelmat. Kerran toinen tiedemies, Galileo Galilei, kiinnostui Aristoteleen teoksista. Yksi Aristoteleen perusteesistä oli, että kehon liiketapahtuu vain, jos siihen vaikuttaa jokin voima, jonka intensiteetti ja suunta määrää. Galileo osoitti, että tämä oli virhe. Voima vaikuttaa liikenopeusparametriin, mutta ei enempää. Italialainen osoitti, että voima on kiihtyvyyden syy, ja se voi syntyä vain molemminpuolisesti sen kanssa. Myös Galileo Galilei kiinnitti huomattavaa huomiota vapaan pudotuksen prosessin tutkimukseen ja johdatti asianmukaiset mallit. Luultavasti kaikki muistavat hänen kuuluisat kokeensa, jotka hän suoritti Pisan k altevassa tornissa. Fyysikko Ampère käytti töissään myös kinemaattisten ratkaisujen perusteita.
Alkukäsitteet
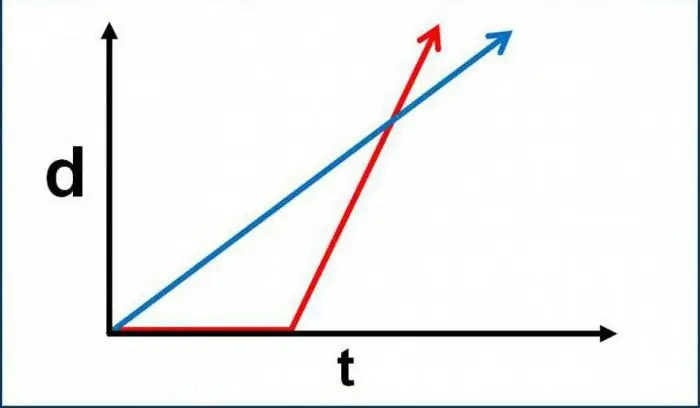
Kuten aiemmin mainittiin, kinematiikka tutkii tapoja kuvata idealisoitujen esineiden liikettä. Tällöin matemaattisen analyysin perusteita, tavallista algebraa ja geometriaa voidaan soveltaa käytännössä. Mutta mitkä käsitteet (täsmälleen käsitteet, ei parametristen suureiden määritelmät) ovat tämän fysiikan alaosan taustalla? Ensinnäkin jokaisen tulee ymmärtää selvästi, että materiaalipisteen translaatioliikkeen kinematiikka ottaa huomioon liikkeen ottamatta huomioon voimaindikaattoreita. Eli vastaavien ongelmien ratkaisemiseksi emme tarvitse voimaon liittyviä kaavoja. Kinematiikka ei ota sitä huomioon, riippumatta siitä kuinka monta niitä on - yksi, kaksi, kolme, vähintään useita satojatuhansia. Siitä huolimatta kiihtyvyyden olemassaolo on edelleen mahdollista. Useissa ongelmissa aineellisen pisteen liikkeen kinematiikka määrää kiihtyvyyden suuruuden. Kuitenkin tämän ilmiön syyt (eli voimat janiiden luonnetta) ei oteta huomioon vaan jätetään pois.
Luokittelu
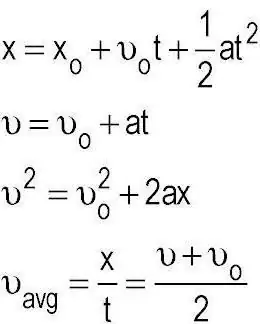
Havaitsimme, että kinematiikka tutkii ja soveltaa menetelmiä kappaleiden liikkeen kuvaamiseen ottamatta huomioon niihin vaikuttavia voimia. Muuten, toinen mekaniikan alaosasto, jota kutsutaan dynamiikaksi, käsittelee tällaista tehtävää. Jo siellä sovelletaan Newtonin lakeja, joiden avulla voidaan käytännössä määrittää melko paljon parametreja pienellä määrällä tunnettuja lähtötietoja. Aineellisen pisteen kinematiikan peruskäsitteet ovat tila ja aika. Ja tieteen kehityksen yhteydessä sekä yleisesti että tällä alueella heräsi kysymys tällaisen yhdistelmän käytön tarkoituksenmukaisuudesta.
Alusta alkaen oli klassista kinematiikkaa. Voimme sanoa, että sille ei ole ominaista vain sekä ajallisten että tilallisten aukkojen läsnäolo, vaan myös niiden riippumattomuus yhden tai toisen viitekehyksen valinnasta. Muuten, puhumme tästä hieman myöhemmin. Selitetään nyt vain, mistä puhumme. Tässä tapauksessa segmenttiä pidetään tilavälinä ja aikaväliä ajallisena intervallina. Kaikki näyttää olevan selvää. Joten näitä aukkoja pidetään klassisessa kinematiikassa absoluuttisina, muuttumattomina, toisin sanoen riippumattomina siirtymisestä viitekehyksestä toiseen. Olipa liiketoiminnan relativistinen kinematiikka. Siinä aukot referenssijärjestelmien välisen siirtymisen aikana voivat muuttua. Olisi jopa oikeampaa sanoa, että he eivät voi, mutta heidän täytyy luultavasti. Tästä johtuen näiden kahden samanaikaisuussatunnaisista tapahtumista tulee myös suhteellisia ja erityishuomiota. Siksi relativistisessa kinematiikassa kaksi käsitettä - tila ja aika - yhdistetään yhdeksi.
Aineellisen pisteen kinematiikka: nopeus, kiihtyvyys ja muut suureet
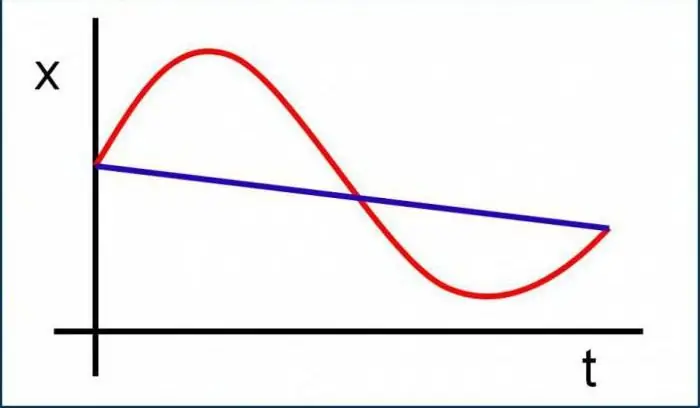
Ymmärtääksesi ainakin vähän tätä fysiikan alaosaa, sinun on navigoitava tärkeimmät käsitteet, tunnettava määritelmät ja kuviteltava, mikä tämä tai tuo suure on yleisesti ottaen. Tässä ei ole mitään vaikeaa, itse asiassa kaikki on erittäin helppoa ja yksinkertaista. Harkitse ehkä aluksi kinemaattisissa tehtävissä käytettyjä peruskäsitteitä.
Liike
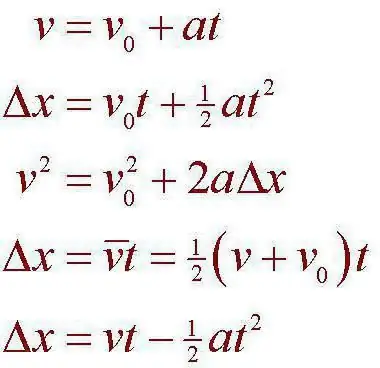
Mekaanista liikettä tarkastellaan prosessia, jonka aikana yksi tai toinen idealisoitu esine muuttaa sijaintiaan avaruudessa. Tässä tapauksessa voimme sanoa, että muutos tapahtuu suhteessa muihin kehoihin. On myös tarpeen ottaa huomioon, että tietyn aikavälin asettaminen kahden tapahtuman välillä tapahtuu samanaikaisesti. On esimerkiksi mahdollista eristää tietty aika, joka muodostuu kehon asennosta toiseen saapumisen välillä. Huomaa myös, että kehot voivat tässä tapauksessa olla vuorovaikutuksessa toistensa kanssa mekaniikan yleisten lakien mukaisesti. Juuri tällä materiaalipisteen kinematiikka useimmiten toimii. Viitejärjestelmä on seuraava käsite, joka liittyy siihen erottamattomasti.
Koordinaatit
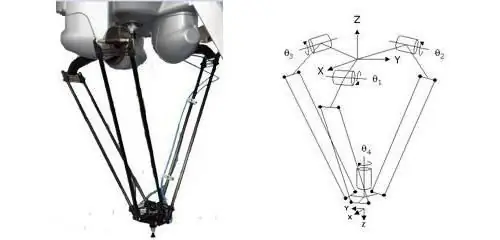
Niitä voidaan kutsua tavallisiksi tiedoiksi, joiden avulla voit määrittää kehon sijainnin kerralla tai toisella. Koordinaatit liittyvät erottamattomasti referenssijärjestelmän käsitteeseen sekä koordinaattiverkkoon. Useimmiten ne ovat kirjainten ja numeroiden yhdistelmä.
Sädevektori
Nimestä pitäisi jo olla selvää, mikä se on. Puhutaanpa tästä kuitenkin tarkemmin. Jos piste liikkuu tiettyä lentorataa pitkin ja tiedämme tarkalleen tietyn referenssijärjestelmän alun, voimme piirtää sädevektorin milloin tahansa. Se yhdistää pisteen alkupaikan hetkelliseen tai lopulliseen sijaintiin.
Rata
Sitä kutsutaan jatkuvaksi viivaksi, joka lasketaan materiaalipisteen liikkeen seurauksena tietyssä vertailujärjestelmässä.
Nopeus (sekä lineaarinen että kulma)
Tämä on arvo, joka voi kertoa, kuinka nopeasti keho kulkee tietyn välimatkan läpi.
Kiihtyvyys (sekä kulma- että lineaarinen)
Näyttää minkä lain mukaan ja kuinka voimakkaasti kehon nopeusparametri muuttuu.
Ehkä tässä ne ovat - materiaalipisteen kinematiikan pääelementit. On huomattava, että sekä nopeus että kiihtyvyys ovat vektorisuureita. Ja tämä tarkoittaa, että niillä ei ole vain ohjeellista arvoa, vaan myös tietty suunta. Muuten, ne voidaan suunnata sekä yhteen suuntaan että vastakkaisiin suuntiin. Ensimmäisessä tapauksessa keho kiihtyy, toisessa se hidastuu.
Yksinkertaiset tehtävät
Aineellisen pisteen kinematiikka (nopeus, kiihtyvyys ja etäisyys ovat käytännössä peruskäsitteitä) sisältää paitsi v altavan määrän tehtäviä, myös monia niiden eri luokkia. Yritetään ratkaista melko yksinkertainen ongelma määrittämällä kehon kulkema matka.
Oletetaan, että meillä on seuraavat ehdot. Kuljettajan auto on lähtöviivalla. Kuljettaja antaa lupaa lipulla, ja auto lähtee äkillisesti liikkeelle. Selvitä, pystyykö hän tekemään uuden ennätyksen kilpailijoiden kilpailussa, jos seuraava johtaja kulki sadan metrin matkan 7,8 sekunnissa. Otetaan auton kiihtyvyys, joka on 3 metriä jaettuna sekuntineliöllä.
Miten ratkaistaan tämä ongelma? Se on varsin mielenkiintoista, koska meidän ei tarvitse "kuivaa" määrittää tiettyjä parametreja. Sitä kirkastaa liikevaihdot ja tietty tilanne, joka monipuolistaa ratkaisemisen ja indikaattoreiden etsimisen prosessia. Mutta mitä meidän tulisi ohjata ennen kuin ryhdymme tehtävään?
1. Materiaalipisteen kinematiikka mahdollistaa kiihtyvyyden käytön tässä tapauksessa.
2. Ratkaisu oletetaan käyttämällä etäisyyskaavaa, koska sen numeerinen arvo näkyy ehdoissa.
Ongelma on itse asiassa ratkaistu melko yksinkertaisesti. Tätä varten otamme etäisyyskaavan: S=VoT + (-) AT ^ 2/2. Mikä on pointti? Meidän on selvitettävä, kuinka kauan ratsastaja kulkee määrätyn matkan, ja sitten vertaa lukua ennätykseen saadaksemme selville, voittaako hän sen vai ei. Tätä varten varaa aika, saamme kaavanhänelle: AT^2 + 2VoT - 2S. Tämä ei ole muuta kuin toisen asteen yhtälö. Mutta auto lähtee liikkeelle, mikä tarkoittaa, että alkunopeus on 0. Yhtälöä ratkaistaessa diskriminantti on 2400. Ajan löytämiseksi sinun on otettava juuri. Tehdään se toisen desimaalin tarkkuudella: 48,98 Etsi yhtälön juuri: 48,98/6=8,16 sekuntia. Osoittautuu, että kuljettaja ei pysty lyömään nykyistä ennätystä.






