Jokainen koululainen tietää, että valo homogeenisessa läpinäkyvässä väliaineessa liikkuu suoraa tietä. Tämä tosiasia antaa meille mahdollisuuden tarkastella monia optisia ilmiöitä valonsäteen käsitteen puitteissa. Tässä artikkelissa kerrotaan säteen tulokulmasta ja siitä, miksi on tärkeää tietää tämä kulma.
Valonsäde on mikrometrin sähkömagneettinen a alto
Fysiikassa on erilaisia a altoja: ääni-, meri-, sähkömagneettisia ja joitain muita. Termi "säde" koskee kuitenkin vain sähkömagneettisia a altoja, joista näkyvä spektri on osa. Itse sana "säde" voidaan esittää suorana, joka yhdistää kaksi pistettä avaruudessa.
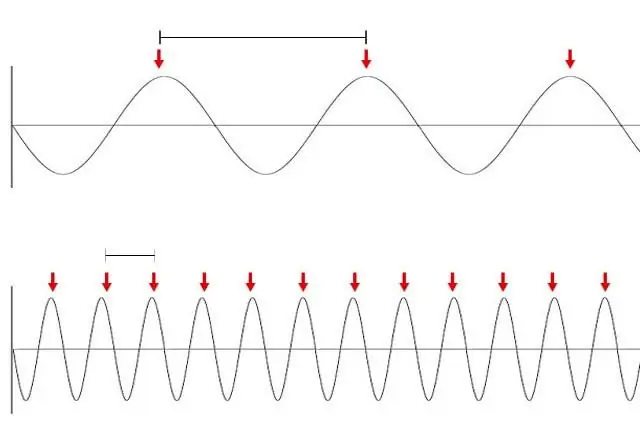
Valo (aallona) voidaan nähdä suorana viivana, koska jokainen a alto viittaa värähtelyjen esiintymiseen. Vastaus tähän kysymykseen on aallonpituuden arvossa. Joten meren ja äänen os alta pituus vaihtelee muutamasta senttimetreistä kymmeniin metriin. Tietenkin tällaisia värähtelyjä tuskin voidaan kutsua säteeksi. Valon aallonpituus on alle yksi mikrometri. Ihmissilmä ei pysty erottamaan tällaisia värähtelyjä, joten meistä näyttää siltäettä näemme suoran säteen.
Täydentävyyden vuoksi on huomattava, että valonsäde on näkyvissä vain silloin, kun se alkaa sirotella pieniä hiukkasia, kuten pölyisessä huoneessa tai sumupisaroissa.
Missä on tärkeää tietää kulma, jossa säde osuu esteeseen?
Heijastumisen ja taittumisen ilmiöt ovat tunnetuimpia optisia efektejä, joita ihminen kohtaa kirjaimellisesti joka päivä, kun hän katsoo itseään peilistä tai juo lasin teetä katsottuaan siinä olevaa lusikkaa.
Taittumisen ja heijastuksen matemaattinen kuvaus edellyttää säteen tulokulman tuntemista. Esimerkiksi heijastusilmiölle on tunnusomaista heijastuskulman ja tulokulman yhtäläisyys. Jos kuvataan taittumisprosessin puolelta, tulokulma ja taitekulma liittyvät toisiinsa sinien funktioiden ja median taitekertoimien kautta (Snellin laki).

Kulmalla, jossa valonsäde osuu kahden läpinäkyvän materiaalin väliseen rajapintaan, on tärkeä rooli, kun tarkastellaan sisäisen kokonaisheijastuksen vaikutusta optisesti tiheämmässä materiaalissa. Tämä vaikutus havaitaan vain tulokulmissa, jotka ovat suurempia kuin jokin kriittinen arvo.
Tarkastellun kulman geometrinen määritelmä
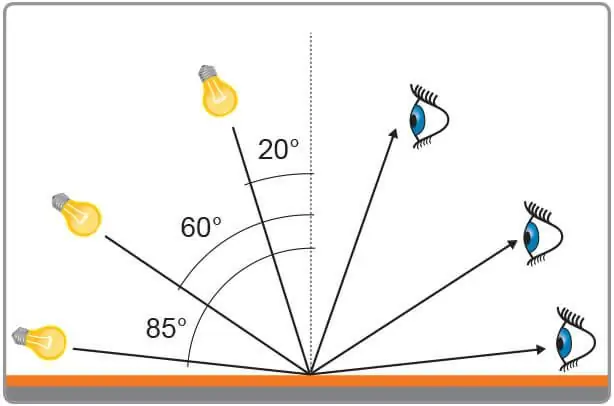
Voidaan olettaa, että on olemassa pinta, joka erottaa nämä kaksi ympäristöä. Tämä pinta voi olla tasainen, kuten peilin tapauksessa, tai se voi olla monimutkaisempi, kuten meren harjuinen pinta. Kuvittele, että tälle pinnalle putoaavalokeila. Kuinka määrittää valon tulokulma? Tämän tekeminen on melko yksinkertaista. Seuraavassa on toimintosarja, joka tulee tehdä halutun kulman löytämiseksi.
- Ensin sinun on määritettävä säteen ja pinnan leikkauspiste.
- O:n kautta tulee piirtää kohtisuora tarkasteltuun pintaan. Sitä kutsutaan usein normaaliksi.
- Säteen tulokulma on yhtä suuri kuin sen ja normaalin välinen kulma. Se voidaan mitata yksinkertaisella astemittarilla.
Kuten näet, harkitun kulman löytäminen ei ole vaikeaa. Oppilaat tekevät kuitenkin usein sen virheen mittaaessaan sen tason ja säteen välistä. On muistettava, että tulokulma mitataan aina normaalista riippumatta pinnan muodosta ja väliaineesta, jossa se etenee.
Pyöreät peilit, linssit ja niihin putoavat säteet
Tietoa tiettyjen säteiden tulokulmien ominaisuuksista käytetään kuvien rakentamisessa pallomaisissa peileissä ja ohuissa linsseissä. Tällaisten kuvien rakentamiseksi riittää tietää, kuinka kaksi erilaista sädettä käyttäytyvät vuorovaikutuksessa nimettyjen optisten laitteiden kanssa. Näiden säteiden leikkauskohta määrittää kuvapisteen sijainnin. Yleensä löytyy aina kolme erilaista sädettä, joiden kulku on tarkasti tiedossa (kolmannen säteen avulla voidaan tarkistaa konstruoidun kuvan oikeellisuus). Nämä säteet on nimetty alla.
- Kulkee yhdensuuntaisesti laitteen optisen pääakselin kanssa. Se kulkee tarkennuksen läpi heijastuksen tai taittuman jälkeen.
- Laitteen fokuksen läpi kulkeva säde. Se heijastuu ainataitettu samansuuntaisesti pääakselin kanssa.
- Optisen keskustan läpi kulkeminen (pallomaisessa peilissä se osuu pallon keskustaan, linssillä se on sen sisällä). Tällainen säde ei muuta sen lentorataa.
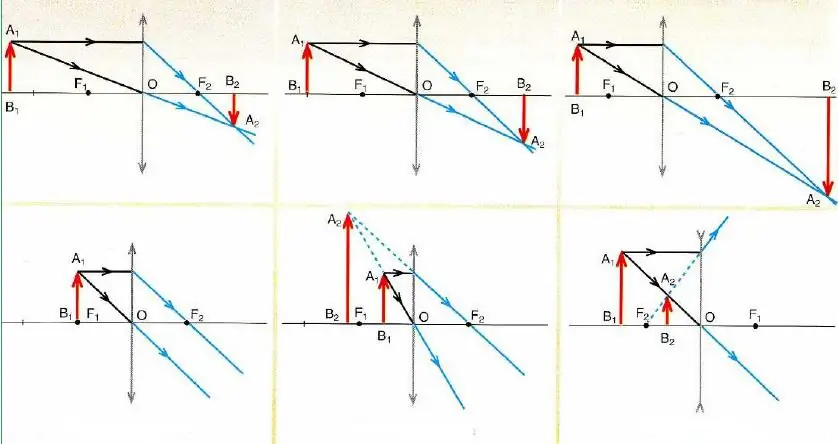
Yllä oleva kuva näyttää kaaviot kuvien rakentamiseen eri vaihtoehdoille kohteen sijainnille suhteessa ohuisiin linsseihin.






