Grand Unified Theory (GUT, GUT tai GUT - kaikkia kolmea lyhennettä käytetään artikkelissa) on hiukkasfysiikan malli, jossa suurella energialla vakiomallin kolme mittausvaikutusta, jotka määrittävät sähkömagneettisen, heikko ja vahva vuorovaikutus tai voima yhdistetään yhdeksi voimaksi. Tälle yhdistetylle vuorovaikutukselle on tunnusomaista yksi suurempi symmetria ja siksi useita kantovoimaa, mutta yksi pysyvä sidos. Jos luonnossa tapahtuu suuri yhdistyminen, varhaisessa universumissa on mahdollisuus suureen yhdistymisen aikakauteen, jossa perusvoimat eivät ole vielä erilaisia.
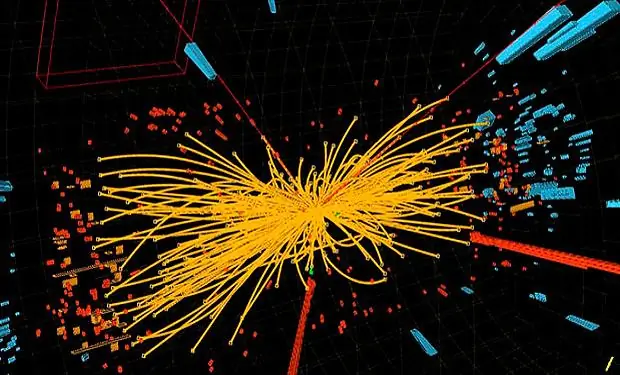
Suuri yhtenäinen teoria lyhyesti
Mallit, jotka eivät yhdistä kaikkia vuorovaikutuksia käyttämällä yhtä yksinkertaista ryhmää mittaussymmetriana, tekevät niin käyttämällä puoliyksinkertaisia ryhmiä, niillä voi olla samanlaisia ominaisuuksia ja niitä kutsutaan joskus myös suuriksi yhdistämisteorioiksi.
Painovoiman yhdistäminen kolmen muun voiman kanssa antaisi teorian kaikesta (OO) GUT:n sijaan. GUT nähdään kuitenkin usein väliaskeleena kohti OO:ta. Nämä ovat kaikki tyypillisiä ideoita suurille yhdentymisen ja superyhdistämisen teorioille.
GUT-mallien ennustamien uusien hiukkasten massojen odotetaan olevan GUT-asteikon ympärillä - vain muutaman suuruusluokan Planckin asteikon alapuolella - ja siksi ne ovat ulottumattomissa ehdotetuille hiukkasten törmäyskokeille. Siksi GUT-mallien ennustamia hiukkasia ei voida tarkkailla suoraan, vaan suuret yhdistämisvaikutukset voidaan havaita epäsuorien havaintojen, kuten protonien hajoamisen, alkeishiukkasten sähköisten dipolimomenttien tai neutrino-ominaisuuksien avulla. Jotkut GUT:t, kuten Pati Salam -malli, ennustavat magneettisten monopolien olemassaolon.
Mallejen ominaisuudet
GUT-mallit, jotka pyrkivät olemaan täysin realistisia, ovat varsin monimutkaisia jopa standardimalliin verrattuna, koska niissä on esitettävä lisäkenttiä ja vuorovaikutuksia tai jopa lisätilaa. Pääsyy tähän monimutkaisuuteen on havaittujen fermionimassojen ja sekoituskulmien toistamisen vaikeudessa, mikä saattaa johtua joistakin lisäperhesymmetrioista perinteisten GUT-mallien ulkopuolella. Tämän vaikeuden ja havaittavan suuren yhdistämisvaikutuksen puuttumisen vuoksi ei ole vieläkään yleisesti hyväksyttyä GUT-mallia.

Historiallisesti ensintodellista GUT:ta, joka perustuu Leen yksinkertaiseen SU-ryhmään, ehdottivat Howard George ja Sheldon Glashow vuonna 1974. Georgi-Glashow-mallia edelsi puoliyksinkertaisen Lie-algebran Pati-Salam-malli, jonka ehdottivat Abdus Salam ja Jogesh Pati, joka ehdotti ensimmäisenä yhdistäviä mittarien vuorovaikutuksia.
Nimihistoria
Lyhenteen GUT (GUT) keksivät ensimmäisen kerran CERNin tutkijat John Ellis, Andrzej Buras, Mary C. Gayard ja Dmitry Nanopoulos vuonna 1978, mutta artikkelinsa lopullisessa versiossa he valitsivat GUM:n (great Unification mass). Nanopoulos käytti myöhemmin samana vuonna ensimmäisenä lyhennettä artikkelissa. Lyhyesti sanottuna, paljon työtä on tehty matkalla kohti Grand Unified Theorya.

Käsitteiden yleisyys
Lyhennettä SU käytetään viittaamaan suuriin yhdistämisteorioihin, joihin viitataan usein tässä artikkelissa. Se tosiasia, että elektronien ja protonien sähkövaraukset näyttävät kumoavan toisensa äärimmäisellä tarkkuudella, on oleellista makroskooppiselle maailmalle sellaisena kuin me sen tunnemme, mutta tätä alkuainehiukkasten tärkeää ominaisuutta ei selitetä hiukkasfysiikan vakiomallissa. Vaikka standardimallin vahvojen ja heikkojen vuorovaikutusten kuvaus perustuu mittasymmetrioihin, joita hallitsevat yksinkertaiset SU(3) ja SU(2) symmetriaryhmät, jotka sallivat vain erilliset varaukset, jäljellä oleva komponentti, heikko hypervarausvuorovaikutus, on kuvattu Abelin U(1), mikä periaatteessa salliimaksujen mieliv altainen jakautuminen.

Havaittu varauskvantisointi, nimittäin se tosiasia, että kaikissa tunnetuissa alkuainehiukkasissa on sähkövarauksia, jotka näyttävät olevan tarkat kerrannaiset alkeisvarauksesta, johti ajatukseen, että ylivarausvuorovaikutuksia ja mahdollisesti vahvoja ja heikkoja vuorovaikutuksia voitaisiin rakentaa yhdeksi suureksi yhtenäiseksi vuorovaikutukseksi, jota kuvaa yksi suurempi yksinkertainen symmetriaryhmä, joka sisältää vakiomallin. Tämä ennustaa automaattisesti alkuainehiukkasten kaikkien varausten kvantisoidun luonteen ja arvot. Koska se johtaa myös havaitsemiemme taustalla olevien vuorovaikutusten, erityisesti heikon sekoituskulman, suhteellisten vahvuuksien ennustamiseen, Grand Unification vähentää ihanteellisesti riippumattomien syötteiden määrää, mutta rajoittuu myös havaintoihin. Niin universaalilta kuin suuri yhtenäinen teoria saattaakin näyttää, sitä käsittelevät kirjat eivät ole kovin suosittuja.
Georgie-Glasgow'n teoria (SU (5))
Suuri yhdistäminen muistuttaa sähköisten ja magneettisten voimien yhdistämistä Maxwellin sähkömagnetismiteoriassa 1800-luvulla, mutta sen fyysinen merkitys ja matemaattinen rakenne ovat laadullisesti erilaiset.
Ei kuitenkaan ole ilmeistä, että yksinkertaisin mahdollinen valinta laajennetun suuren yhtenäisen symmetrian saavuttamiseksi on tuottaa oikea joukko alkuainehiukkasia. Se tosiasia, että kaikki tällä hetkellä tunnetut aineen hiukkaset sopivat hyvin kolmeen pienimpään SU(5)-ryhmän esitysteoriaan ja kantavat välittömästi oikeita havaittavia varauksia, on yksi ensimmäisistä jatärkeimmät syyt, miksi ihmiset uskovat, että suuri yhtenäinen teoria voidaan todella toteuttaa luonnossa.

SU(5):n kaksi pienintä pelkistymätöntä esitystä ovat 5 ja 10. Vakiomerkinnöissä 5 sisältää oikeanpuoleisen alas-tyyppisen väritripletin ja vasen-vasemman isospin-dupletin varauskonjugaatit, kun taas 10 sisältää kuusi komponenttia ylös-tyypin kvarkista, väritä vasemman käden alas-tyypin kvarkin tripletti ja oikeakätinen elektroni. Tämä kaavio on toistettava jokaiselle tunnetulle ainesukupolvelle. On huomionarvoista, että teoria ei sisällä tämän sisällön poikkeavuuksia.
Hypoteettiset oikeakätiset neutriinot ovat SU(5) singletti, mikä tarkoittaa, että sen massaa ei kielletä mikään symmetria; sen ei tarvitse spontaanisti rikkoa symmetriaa, mikä selittää, miksi sen massa on suuri.
Tässä aineen yhdistyminen on vielä täydellisempää, koska pelkistymätön spinoriesitys 16 sisältää sekä 5:n että 10:n SU(5) ja oikeakätisten neutriinojen ja siten yhden sukupolven hiukkasten kokonaissisällön. laajennettu vakiomalli neutriinomassalla. Tämä on jo suurin yksinkertainen ryhmä, joka saavuttaa aineen yhdistämisen järjestelmässä, joka sisältää vain jo tunnetut aineen hiukkaset (paitsi Higgsin sektori).
Koska erilaiset standardimallifermionit on ryhmitelty suurempiin esityksiin, GUT:t ennustavat erityisesti fermionimassojen välisiä suhteita, kuten elektronin jauntuvakvarkki, muuoni ja outo kvarkki sekä tau leptoni ja untuvakvarkki SU:lle(5). Jotkut näistä massasuhteista ovat likimääräisiä, mutta useimmat eivät.

SO(10) teoria
SO(10):n bosonimatriisi löydetään ottamalla SU(5):n 10 + 5 esitys 15 × 15 -matriisi ja lisäämällä ylimääräinen rivi ja sarake oikealle neutriinolle. Bosonit voidaan löytää lisäämällä kumppani jokaiseen 20 varautuneeseen bosoniin (2 oikeaa W-bosonia, 6 massiivisesti varautunutta gluonia ja 12 X/Y-tyyppistä bosonia) ja lisäämällä ylimääräinen raskas neutraali Z-bosoni, jolloin muodostuu 5 neutraalia bosonia. Bosonisen matriisin jokaisella rivillä ja sarakkeella on bosoni tai sen uusi kumppani. Nämä parit yhdessä luovat tutut 16D Dirac -spinmatriisit SO(10).
Vakiomalli
Vakiomallin ei-kiraaliset laajennukset jakautuneiden multiplettihiukkasten vektorispektreillä, joita esiintyy luonnollisesti korkeammissa SU(N) GUT:issa, muuttavat merkittävästi aavikon fysiikkaa ja johtavat realistiseen (rivimittakaavaiseen) suureen yhdistymiseen tavalliselle kolmelle kvarkki-leptonille perheille jopa ilman supersymmetriaa (katso alla). Toisa alta uuden puuttuvan VEV-mekanismin ilmaantuessa supersymmetriseen SU(8) GUT:hen, voidaan löytää samanaikainen ratkaisu mittarihierarkiaongelmaan (doublet-triplet splitting) ja makuyhdistämisongelmaan.
Muut teoriat ja alkuainehiukkaset
GUT neljällä perheellä/sukupolvella, SU(8): oletetaan, että 4 sukupolvea fermioneja kolmen sijasta tuottaa yhteensä 64 hiukkastyyppiä. Ne voidaan sijoittaa 64=8 + 56 SU(8) -esitykseen. Tämä voidaan jakaa SU(5) × SU(3) F × U(1), joka on SU(5) teoria, sekä joitakin raskaita bosoneja, jotka vaikuttavat sukupolvien lukumäärään.
GUT neljällä perheellä/sukupolvella, O(16): Jälleen, olettaen 4 sukupolvea fermioneja, 128 hiukkasta ja antihiukkasta mahtuvat yhteen O(16)-spinoriesitykseen. Kaikki nämä asiat löydettiin matkalla kohti suurta yhtenäistä teoriaa.






