Kuten tiedät, mikä tahansa fyysinen suure kuuluu johonkin kahdesta tyypistä, se on joko skalaari tai vektori. Tässä artikkelissa tarkastelemme sellaisia kinemaattisia ominaisuuksia kuin nopeutta ja kiihtyvyyttä, ja näytämme myös mihin kiihtyvyys- ja nopeusvektorit ovat suunnattu.
Mitä on nopeus ja kiihtyvyys?
Molemmat tässä kappaleessa mainitut suureet ovat tärkeitä ominaisuuksia kaikenlaiselle liikkeelle, olipa kyseessä sitten kappaleen liikuttaminen suorassa linjassa tai kaarevaa polkua pitkin.
Nopeus on nopeus, jolla koordinaatit muuttuvat ajan myötä. Matemaattisesti tämä arvo on yhtä suuri kuin kuljetun matkan aikaderivaata, eli
v¯=dl¯/dt.
Tässä vektori l¯ on suunnattu polun alkupisteestä loppupisteeseen.
Kiihtyvyys puolestaan on nopeus, jolla itse nopeus muuttuu ajassa. Kaavan muodossa se voidaan kirjoittaa näin:
a¯=dv¯/dt.
Ilmeisesti ottaen toisen johdannaisensiirtymävektori l¯ ajassa, saamme myös kiihtyvyyden arvon.
Koska nopeus mitataan metreinä sekunnissa, kiihtyvyys mitataan kirjoitetun lausekkeen mukaan metreinä sekunnissa neliö.

Missä ovat kiihtyvyys- ja nopeusvektorit?
Fysiikassa jokaiselle kehon mekaaniselle liikkeelle on yleensä tunnusomaista tietty liikerata. Jälkimmäinen on jokin kuvitteellinen käyrä, jota pitkin keho liikkuu avaruudessa. Esimerkiksi suora tai ympyrä ovat hyviä esimerkkejä yleisistä liikereiteistä.
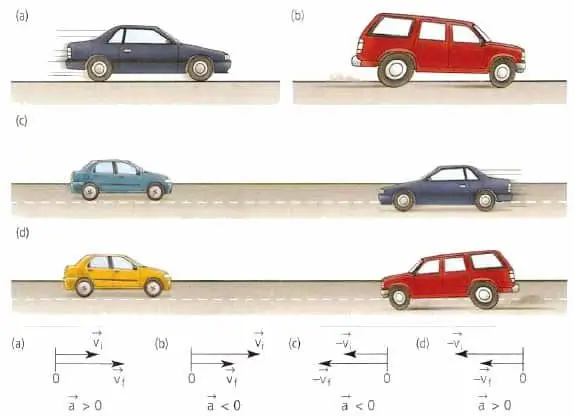
Kehon nopeusvektori on aina suunnattu liikkeen suuntaan, riippumatta siitä, hidastaako vai kiihtyykö keho, liikkuuko se suorassa linjassa vai kaaressa. Geometrisesti sanottuna nopeusvektori on suunnattu tangentiaalisesti siihen lentoradan pisteeseen, jossa kappale tällä hetkellä sijaitsee.
Materiaalin tai kappaleen pisteen kiihtyvyysvektorilla ei ole mitään tekemistä nopeuden kanssa. Tämä vektori on suunnattu nopeuden muutoksen suuntaan. Esimerkiksi suoraviivaisessa liikkeessä arvo a¯ voi joko yhtyä suuntaan v¯:n kanssa tai olla vastakkainen v¯:n kanssa.
Kehoon vaikuttava voima ja kiihtyvyys
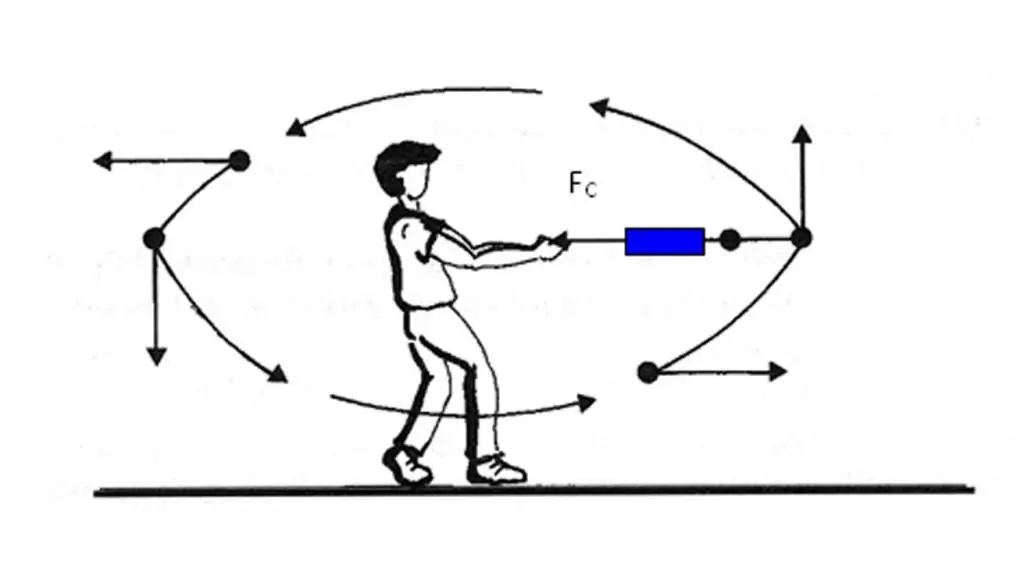
Olemme havainneet, että kappaleen kiihtyvyysvektori on suunnattu kohti nopeusvektorin muutosta. Aina ei kuitenkaan ole helppoa määrittää, kuinka nopeus muuttuu tietyssä lentoradan pisteessä. Lisäksi nopeuden muutoksen määrittämiseksi on tarpeen suorittaa toimenpidevektorierot. Näiden vaikeuksien välttämiseksi vektorin a¯ suunnan määrittämisessä on toinen tapa selvittää nopeasti.
Alla on Newtonin kuuluisa ja jokaiselle opiskelijalle tuttu laki:
F¯=ma¯.
Kaava osoittaa, että kappaleiden kiihtyvyyden syy on niihin vaikuttava voima. Koska massa m on skalaari, voimavektori F¯ ja kiihtyvyysvektori a¯ ovat samassa suunnassa. Tämä tosiasia tulee muistaa ja soveltaa käytännössä aina, kun on tarve määrittää suuren suunta a¯.
Jos kehoon vaikuttaa useita erilaisia voimia, niin kiihtyvyysvektorin suunta on yhtä suuri kuin kaikkien voimien tuloksena oleva vektori.
Ympyräliike ja kiihtyvyys
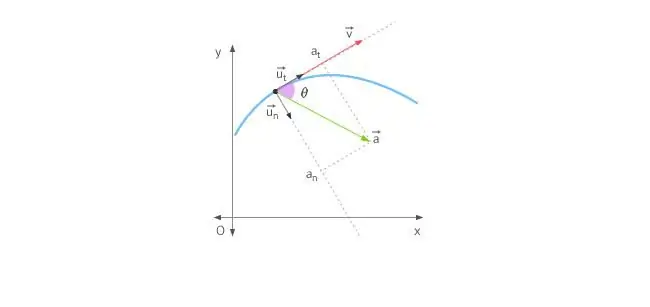
Kun kappale liikkuu suorassa linjassa, kiihtyvyys suunnataan joko eteen- tai taaksepäin. Ympyrässä tapahtuvan liikkeen tapauksessa tilannetta mutkistaa se, että nopeusvektori muuttaa jatkuvasti suuntaansa. Edellä esitetyn perusteella kokonaiskiihtyvyys määräytyy sen kahdella komponentilla: tangentiaalisella ja normaalikiihtyvyydellä.
Tangiaalinen kiihtyvyys on suunnattu täsmälleen samalla tavalla kuin nopeusvektori, tai sitä vastaan. Toisin sanoen tämä kiihtyvyyskomponentti on suunnattu lentoradan tangenttia pitkin. Tangentiaalinen kiihtyvyys kuvaa muutosta itse nopeuden moduulissa.
Normaalikiihtyvyys suunnataan normaalia pitkin liikeradan annettuun pisteeseen ottaen huomioon sen kaarevuus. Jos kyseessä on ympyräliike, tämän komponentin vektori osoittaakeskustaan, eli normaalikiihtyvyys on suunnattu pyörimissädettä pitkin. Tätä komponenttia kutsutaan usein keskipisteiseksi.
Täysi kiihtyvyys on näiden komponenttien summa, joten sen vektoria voidaan suunnata mieliv altaisesti ympyräviivan suhteen.
Jos kappale pyörii muuttamatta lineaarinopeutta, on olemassa vain nollasta poikkeava normaalikomponentti, joten koko kiihtyvyysvektori on suunnattu kohti ympyrän keskustaa. Huomaa, että tähän keskustaan vaikuttaa myös voima, joka pitää kehon liikeradalla. Esimerkiksi Auringon gravitaatiovoima pitää maamme ja muut planeettamme kiertoradalla.






