Titius-Boden sääntö (joskus kutsutaan yksinkertaisesti Boden laiksi) on hypoteesi, jonka mukaan kappaleet joissakin kiertoratajärjestelmissä, mukaan lukien Auringossa, pyörivät puoliakseleita pitkin planeettojen järjestyksestä riippuen. Kaava ehdottaa, että ulospäin ulottuva planeetta on noin kaksi kertaa niin kaukana Auringosta kuin edellinen.
Hypoteesi ennusti oikein Ceresin (asteroidivyöhykkeessä) ja Uranuksen kiertoradat, mutta Neptunuksen kiertorataa ei onnistuttu määrittämään, ja se korvattiin lopulta aurinkokunnan muodostumisteorialla. Se on nimetty Johann Daniel Titiuksen ja Johann Elert Boden mukaan.

Origins
Ensimmäinen maininta sarjasta, joka lähestyy Boden lakia, löytyy David Gregoryn Elements of Astronomysta, joka julkaistiin vuonna 1715. Siinä hän sanoo: "…olettaen, että etäisyys Auringosta Maahan on jaettu kymmeneen yhtä suureen osaan, joista Merkuriuksen etäisyys on noin neljä, Venuksesta seitsemän, Marsista viisitoista, Jupiterista viisikymmentäkaksi, ja Saturnuksesta yhdeksänkymmentäviisi". Samanlainen ehdotus, luultavasti Gregoryn innoittama, esiintyy Christian Wolffin vuonna 1724 julkaisemassa teoksessa.
Vuonna 1764 Charles Bonnet sanoi kirjassaan Contemplation of Nature: "Tiedämme seitsemäntoista planeettaa, jotka muodostavat aurinkokuntamme [eli pääplaneetat ja niiden satelliitit], mutta emme ole varmoja siitä, että niitä ei ole enää." Tähän Bonnetin teoksen 1766 käännöksessään Johann Daniel Titius lisäsi kaksi omaa kappaletta sivun 7 alareunaan ja sivun 8 yläosaan. Uutta interpoloitua kappaletta ei löydy Bonnet'n alkuperäisestä tekstistä: ei myöskään italiaksi. eikä teoksen englanninkielisiä käännöksiä.
Titiuksen löytö
Titiuksen interkaloidussa tekstissä on kaksi osaa. Ensimmäinen selittää planetaaristen etäisyyksien järjestyksen Auringosta. Se sisältää myös muutaman sanan etäisyydestä Auringosta Jupiteriin. Mutta tämä ei ole tekstin loppu.
On syytä sanoa muutama sana Titius-Boden säännön kaavasta. Kiinnitä huomiota planeettojen välisiin etäisyyksiin ja ota selvää, että melkein kaikki ne ovat erillään toisistaan suhteessa niiden ruumiin kokoon. Jaa etäisyys Auringosta Saturnukseen 100 osalla; silloin Merkuriusta erottaa neljä tällaista osaa Auringosta; Venus - 4 + 3=7 tällaiseen osaan; Maa - 4+6=10; Mars - 4+12=16.
Mutta huomaa, että Marsista Jupiteriin on poikkeama tästä niin tarkasta etenemisestä. Marsista seuraa 4+24=28 tällaisten osien avaruus, mutta toistaiseksi sieltä ei ole löydetty yhtään planeettaa. Mutta pitäisikö Herran arkkitehdin jättää tämä paikka tyhjäksi? Ei koskaan. Niinoletetaan, että tämä avaruus kuuluu epäilemättä Marsin vielä löytämättömiin kuisiin, ja lisätään, että ehkä Jupiterin ympärillä on vielä muutama pienempi kuita, joita ei ole vielä nähty millään kaukoputkella.

Rise of the Bode
Vuonna 1772 Johann Elert Bode, 25-vuotiaana, sai valmiiksi toisen painoksen tähtitieteellisestä kokoelmastaan Anleitung zur Kenntniss des gestirnten Himmels ("Opas tähtitaivaan tuntemiseen"), johon hän lisäsi seuraavan alaviitteen, joka alun perin ei ollut lähdettä, mutta huomattiin myöhemmissä versioissa. Boden muistelmista löytyy viittaus Titiukseen, jossa hänen auktoriteettinsa tunnustetaan selvästi.

Mielipideviesti
Tältä kuulostaa Titius-Boden sääntö jälkimmäisen esittämisessä: jos etäisyys Auringosta Saturnukseen otetaan 100:ksi, Merkurius on erotettu Auringosta neljällä tällaisella osalla. Venus - 4+3=7. Maa - 4+6=10. Mars - 4+12=16.
Nyt on aukko tässä järjestetyssä etenemisessä. Marsin jälkeen seuraa avaruus, jonka laskelma on 4+24=28, jossa ei ole vielä nähty yhtäkään planeettaa. Voimmeko uskoa, että universumin perustaja jätti tämän tilan tyhjäksi? Ei tietenkään. Tästä päästään Jupiterin etäisyyteen laskennan muodossa 4+48=52 ja lopuksi Saturnuksen etäisyyteen - 4+96=100.

Nämä kaksi väitettä, jotka koskevat kaikkia erityisiä typologioita ja kiertoradan säteitä, näyttävät olevan peräisin muinaisista ajoistatähtitiede. Monet näistä teorioista juontavat juurensa ennen 1700-lukua.
Vaikuttaminen
Titius oli saksalaisen filosofin Christian Freiherr von Wolffin (1679-1754) oppilas. Bonnet'n työhön lisätyn tekstin toinen osa perustuu von Wolffin vuoden 1723 teokseen Vernünftige Gedanken von den Wirkungen der Natur.
1900-luvun kirjallisuus antaa Titius-Boden säännön kirjoittajan saksalaiselle filosofille. Jos näin on, Titius voisi oppia häneltä. Toisen vanhemman viittauksen kirjoitti James Gregory vuonna 1702 teoksessaan Astronomiae Physicae et geometryae Elementa, jossa planeettojen etäisyyksistä 4, 7, 10, 16, 52 ja 100 tuli geometrinen eteneminen suhteessa 2.
Tämä on Newtonin lähin kaava, ja se löytyi myös Benjamin Martinin ja Thomas Ceardin kirjoituksista vuosia ennen Bonnetin kirjan julkaisua Saksassa.
Lisätyötä ja käytännön seurauksia
Titius ja Bode toivoivat, että laki johtaisi uusien planeettojen löytämiseen, ja todellakin Uranuksen ja Ceresin löytäminen, joiden välinen etäisyys on hyvin lain mukainen, vaikutti siihen, että tiedemaailma hyväksyi sen.
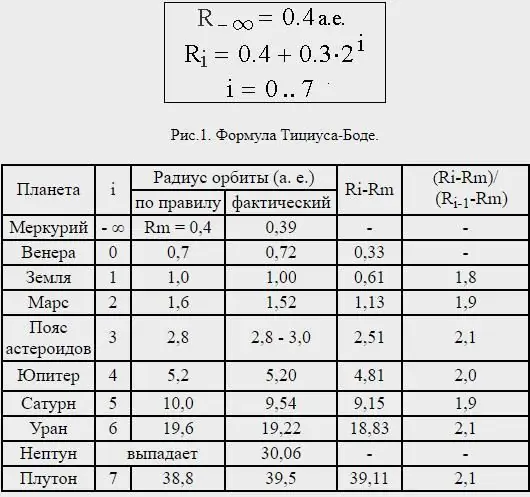
Neptunuksen etäisyys oli kuitenkin hyvin epäjohdonmukainen, ja itse asiassa Pluto - jota nyt ei pidetä planeetana - on keskimääräisellä etäisyydellä, joka vastaa suunnilleen Titius-Boden lakia, joka on ennustettu seuraavalle Uranuksen ulkopuolella olevalle planeetalle.
Alun perin julkaistun lain täyttivät suunnilleen kaikki tunnetut planeetat - Merkurius ja Saturnus - erollaneljäs ja viides planeetta. Tätä pidettiin mielenkiintoisena, mutta ei erityisen tärkeänä hahmona, kunnes Uranus löydettiin vuonna 1781, mikä sopii sarjaan.
Tämän löydön perusteella Bode kehotti etsimään viidettä planeettaa. Ceres, asteroidivyöhykkeen suurin esine, löydettiin Boden ennustetusta sijainnista vuonna 1801. Boden laki hyväksyttiin laaj alti, kunnes Neptunus löydettiin vuonna 1846 ja sen osoitettiin olevan ristiriidassa lain kanssa.
Samaan aikaan suuri määrä vyöhykkeeltä löydettyjä asteroideja ylitti Ceresin planeettojen luettelosta. Tähtitieteilijä ja loogikko Charles Sanders Peirce käsitteli Boden lakia vuonna 1898 esimerkkinä harhaanjohtavasta päättelystä.

Ongelman kehittyminen
Pluton löytö vuonna 1930 monimutkaisi ongelmaa entisestään. Vaikka se ei vastannut Boden lain ennustamaa asemaa, kyse oli lain Neptunukselle ennustamasta asemasta. Kuiperin vyön myöhempi löytö ja erityisesti objekti Eris, joka on Plutoa massiivisempi, mutta ei kuitenkaan noudata Boden lakia, teki kaavan epäluottamuksen entisestään.
Serdan panos
Jesuiitta Thomas Cerda piti kuuluisan tähtitieteen kurssin Barcelonassa vuonna 1760 Sant Jaume de Cordellen Collegen (Cordellin aatelisten keisarillinen ja kuninkaallinen seminaari) kuninkaallisessa matematiikan katedraalissa. Cerdasin Tratadossa planeettojen etäisyydet esiintyvät, jotka on saatu soveltamalla Keplerin kolmatta lakia, tarkkuudella 10-3.
Jos otamme 10:ksi etäisyyden Maasta japyöristetään ylöspäin kokonaislukuun, geometrinen progressio [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, n=2 arvoon n=8, voidaan ilmaista. Ja käyttämällä ympyränmuotoista yhtenäistä kuvitteellista liikettä Keplerin anomaliaan, kunkin planeetan suhteita vastaavat Rn-arvot voidaan saada muodossa rn=(Rn - R1) / (Rn-1 - R1), jolloin tuloksena on 1,82; 1, 84; 1, 86; 1.88 ja 1.90, joissa rn=2 - 0.02 (12 - n) on eksplisiittinen suhde Keplerin jatkuvuuden ja Titius-Boden lain välillä, jota pidetään satunnaisena numeerisena yhteensattumana. Laskennan tulos on lähellä kahta, mutta kakkosta voidaan hyvin pitää luvun 1 pyöristyksenä 82.

Planeetan keskinopeus n=1:stä n=8:aan pienentää etäisyyttä Auringosta ja eroaa tasaisesta laskusta kohdassa n=2 toipuakseen arvosta n=7 (kiertoradan resonanssi). Tämä vaikuttaa etäisyyteen Auringosta Jupiteriin. Tämä matemaattinen dynamiikka määrää kuitenkin myös kaikkien muiden esineiden välisen etäisyyden sen pahamaineisen säännön puitteissa, jolle artikkeli on omistettu.
Teoreettinen puoli
Titius-Boden säännön taustalla ei ole vankkaa teoreettista selitystä, mutta on mahdollista, että kun otetaan huomioon kiertoradan resonanssin ja vapausasteiden puuttumisen yhdistelmä, mikä tahansa vakaa planeettajärjestelmä toistaa suurella todennäköisyydellä kohdassa kuvatun mallin. tämä kahden tiedemiehen teoria.
Koska tämä voi olla matemaattinen yhteensattuma eikä "luonnonlaki", sitä kutsutaan joskus pikemminkin säännöksi kuin "laiksi". Astrofyysikko Alan Boss kuitenkin väittää, että tämä on yksinkertaisestisattuma, ja planeettatiedelehti Icarus ei enää hyväksy artikkeleita, jotka yrittävät tarjota parannettuja versioita "laista".
Orbitaaliresonanssi
Suurten kiertävien kappaleiden kiertorataresonanssi luo Auringon ympärille alueita, joilla ei ole pitkäaikaista vakaata kiertorataa. Planeetan muodostumisen simulaatiotulokset tukevat ajatusta, että satunnaisesti valittu vakaa planeettajärjestelmä todennäköisesti täyttää Titius-Boden säännön.

Dubrulle ja Graner
Dubrulle ja Graner osoittivat, että potenssilain etäisyyssäännöt voivat olla seurausta planeettajärjestelmien romahtavien pilvien malleista, joilla on kaksi symmetriaa: pyörimisinvarianssi (pilvi ja sen sisältö ovat akselisymmetrisiä) ja mittakaavainvarianssi (pilvi ja sen sisältö näyttää sam alta kaikissa asteikoissa).
Jälkimmäinen on ominaisuus monille ilmiöille, joiden uskotaan vaikuttavan planeetan muodostumiseen, kuten turbulenssiin. Titiuksen ja Boden ehdottamaa etäisyyttä Auringosta aurinkokunnan planeetoihin ei tarkistettu Dubrullen ja Granerin tutkimusten puitteissa.






