Kun vertaisarviointia, esimerkiksi arvioitaessa tuotteiden kilpailukykyä, on, kuten missä tahansa tieteellisessä työssä, tehtävä tilastollinen tietojenkäsittely. Jälkimmäinen alkaa asiantuntijalausuntojen johdonmukaisuuden määrittämisellä, jonka numeerinen ilmaisu on konkordanssikerroin.
Miksi tarvitsemme asiantuntija-konsensusarvioinnin?
Tämä arviointi on tarpeellinen ennen kaikkea siksi, että asiantuntijoiden mielipiteet voivat vaihdella suurestikin arvioiduista parametreista. Aluksi arviointi suoritetaan asettamalla indikaattorit paremmuusjärjestykseen ja antamalla niille tietty merkittävyyskerroin (paino). Epäjohdonmukainen järjestys johtaa siihen, että nämä kertoimet ovat tilastollisesti epäluotettavia. Asiantuntijoiden lausunnot vaaditulla määrällä (yli 7-10) tulee jakaa normaalin lain mukaisesti.
Konkordanssikertoimen käsite
Joten. Johdonmukaisuus on yhdenmukaisuutta. Kerroin on dimensioton suure, joka osoittaa dispersion ja maksimidispersion suhteen yleisessä tapauksessa. Yleistetään nämä käsitteet.
Yhdenmukaisuuskerroin on numero 0-1, joka osoittaa asiantuntijalausuntojen johdonmukaisuuden, kunjoidenkin ominaisuuksien luokittelu. Mitä lähempänä tämä arvo on nollaa, sitä pienempi on konsistenssi. Jos tämän kertoimen arvo on pienempi kuin 0,3, asiantuntijoiden mielipiteitä pidetään epäjohdonmukaisina. Kun kertoimen arvo on välillä 0,3 - 0,7, konsistenssi katsotaan keskimääräiseksi. Arvoa, joka on suurempi kuin 0,7, pidetään yhtenäisenä.
Käyttölaukut
Tilastollista tutkimusta tehtäessä voi syntyä tilanteita, joissa kohdetta voidaan luonnehtia kahdella konkordanssikertoimella tilastollisesti käsitellyllä sekvenssillä, vaan useilla sarjoilla, jotka vastaavasti asiantuntijat, joilla on sama taso ammattitaidolla tietyllä alueella.
Asiantuntijoiden tekemän luokituksen johdonmukaisuus on määritettävä sen hypoteesin paikkansapitävyyden vahvistamiseksi, että asiantuntijat tekevät suhteellisen tarkkoja mittauksia, mikä mahdollistaa erilaisten ryhmittymien muodostumisen asiantuntijaryhmissä, jotka määräytyvät suurelta osin inhimillisistä tekijöistä, pääasiassa erot näkemyksissä, käsitteissä, erilaisissa tieteellisissä koulukunnissa, ammatillisen toiminnan luonteessa jne.
Lyhyt kuvaus sijoitusmenetelmästä. Sen edut ja haitat
Luokittelussa käytetään rank-menetelmää. Sen olemus piilee siinä, että jokaiselle objektin ominaisuudelle on määritetty oma erityinen arvonsa. Lisäksi jokaiselle asiantuntijaryhmään kuuluvalle asiantuntijalle määrätään tämä arvoitsenäisesti, mikä johtaa tarpeeseen käsitellä näitä tietoja asiantuntijalausuntojen johdonmukaisuuden tunnistamiseksi. Tämä prosessi suoritetaan laskemalla yhteensopivuuskerroin.
Rank-menetelmän tärkein etu on sen helppokäyttöisyys.
Menetelmän tärkeimmät haitat ovat:
- pieni määrä sijoituskohteita, koska kun niiden määrä ylittää 15-20, objektiivisten sijoituspisteiden antaminen on vaikeaa;
- Tämän menetelmän käytön perusteella kysymys siitä, kuinka kaukana tutkittavat kohteet ovat toisistaan merkitykseltään, jää avoimeksi.
Tätä menetelmää käytettäessä on otettava huomioon, että luokitukset perustuvat jonkinlaiseen todennäköisyysmalliin, joten niitä tulee soveltaa varoen laajuus huomioon ottaen.
Kendallin yhteensopivuusarvokerroin
Käytetään määrittämään homogeenisia objekteja luonnehtivien kvantitatiivisten ja laadullisten ominaisuuksien välinen suhde ja luokitellaan saman periaatteen mukaan.
Tämä kerroin määritetään kaavalla:
t=2S/(n(n-1)), missä
S - toisen ominaisuuden sekvenssien lukumäärän ja inversioiden lukumäärän välisten erojen summa;
n - havaintojen määrä.

Laskenta-algoritmi:
- X-arvot on järjestetty nousevaan tai laskevaan järjestykseen.
- Y-arvot on järjestetty siihen järjestykseen, jossa ne vastaavat x-arvoja.
- Määritä jokaiselle y:n peräkkäiselle arvolle, kuinka monta korkeampaa arvoa seuraa sitä. Ne lasketaan yhteen ja lasketaan x:n ja y:n järjestysjonojen vastaavuuden mitta.
- Samaan tapaan lasketaan y:n pienempien arvoisten rivien määrä, jotka myös laskevat yhteen.
- Lisää arvoltaan suurempien sarjojen lukumäärä ja pienemmillä arvoilla olevien rivien lukumäärä, jolloin saadaan arvo S.
Tämä kerroin näyttää kahden muuttujan välisen suhteen, ja useimmissa tapauksissa sitä kutsutaan Kendallin rankkorrelaatiokertoimeksi. Tällainen riippuvuus voidaan esittää graafisesti.
kertoimen määrittäminen
Miten se tehdään? Jos rankattujen ominaisuuksien tai tekijöiden määrä ylittää 2, käytetään konkordanssikerrointa, joka pohjimmiltaan on rankkorrelaation moninkertainen muunnelma.
Ole varovainen. Konkordanssikertoimen laskenta perustuu arvoluokkien neliöiden summan poikkeaman keskimääräisestä rivien neliösummasta kerrottuna 12:lla asiantuntijoiden neliöön kerrottuna luvun kuution välisellä erotuksella. kohteista ja objektien määrästä.
Laskenta-algoritmi
Jotta ymmärrämme, mistä laskentakaavan osoittajassa oleva luku 12 tulee, katsotaanpa määritysalgoritmia.
Jokaiselle riville, jolla on tietyn asiantuntijan rivejä, lasketaan rivien summa, joka on satunnainen arvo.
Konkordanssikerroin määritellään yleensä varianssiestimaatin (D) suhteeksi varianssiestimaatin maksimiarvoon.(Dmax). Muotoillaan peräkkäin näiden suureiden määritelmät.
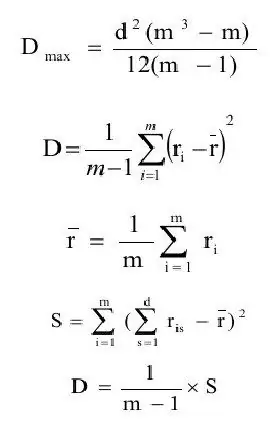
jossa rkeskiarvo - odotusarvio;
m - kohteiden määrä.
Korvaamalla saadut kaavat suhteessa D:hen Dmax saadaan lopullinen kaava konkordanssikertoimelle:
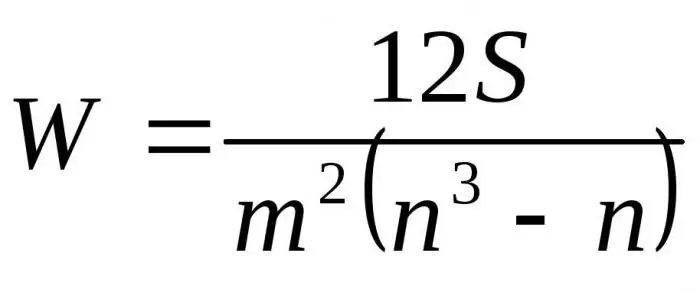
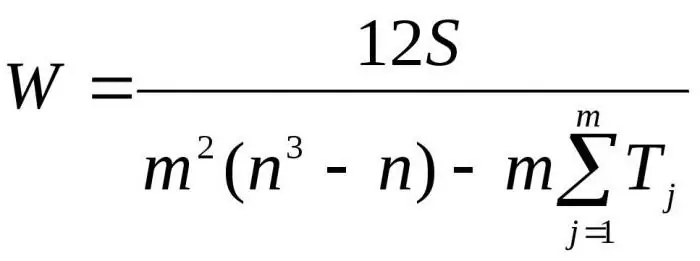
Tässä m on asiantuntijoiden lukumäärä, n on objektien lukumäärä.
Ensimmäistä kaavaa käytetään vastaavuustekijän määrittämiseen, jos toisiinsa liittyviä rivejä ei ole. Toista kaavaa käytetään, jos on toisiinsa liittyviä rivejä.
Joten, konkordanssikertoimen laskenta on ohi. Mitä seuraavaksi? Saadun arvon merkitsevyys arvioidaan Pearson-kertoimella kertomalla tämä kerroin asiantuntijoiden lukumäärällä ja vapausasteiden lukumäärällä (m-1). Saatua kriteeriä verrataan taulukon arvoon, ja jos ensimmäisen arvo ylittää viimeisen, he puhuvat tutkittavan kertoimen merkityksestä.
Suhtautuneiden riveiden tapauksessa Pearson-kriteerin laskemisesta tulee hieman monimutkaisempi ja se suoritetaan seuraavalla suhteella: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Esimerkki
Oletetaan, että asiantuntijamenetelmällä arvioidaan vähittäismyyntiverkostossa myytävän voin kilpailukykyä. Otetaan esimerkki konkordanssikertoimen laskemisesta. Ennen kilpailukyvyn arviointia on tarpeen asettaa kuluttaja paremmuusjärjestykseentämän tuotteen ominaisuudet, jotka ovat mukana arvioinnissa. Oletetaan, että nämä ominaisuudet ovat seuraavat: maku ja tuoksu, koostumus ja ulkonäkö, väri, pakkaus ja merkinnät, rasvapitoisuus, kauppanimi, valmistaja, hinta.
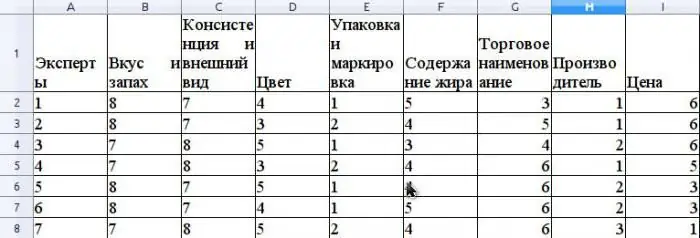
Oletetaan, että asiantuntijaryhmässä on 7 asiantuntijaa. Kuvassa on näiden ominaisuuksien järjestyksen tulokset.
R:n keskiarvo lasketaan aritmeettisena keskiarvona ja se on 31,5. Löytääksesi S, summaa ris ja r-keskiarvon väliset neliöerot kaavan mukaan yllä ja määritä, että S:n arvo on 1718.
Laske yhteensopivuuskerroin kaavalla käyttämättä toisiinsa liittyviä arvoja (sijoitukset olisivat suhteessa, jos samalla Expert Advisorilla olisi samat arvot eri ominaisuuksille).
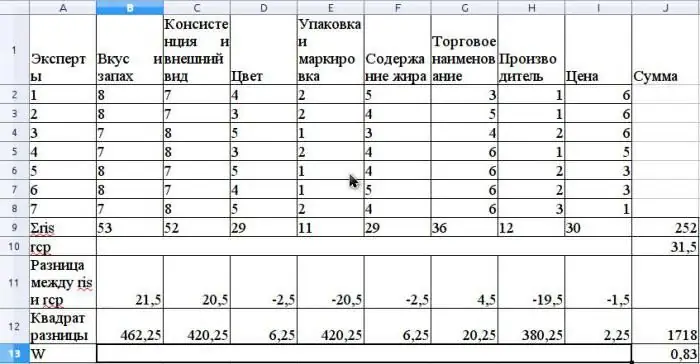
Tämän kertoimen arvo on 0,83. Tämä osoittaa vahvan yksimielisyyden asiantuntijoiden kesken.
Tarkista sen merkitys Pearson-testillä:
7 x 0,83 x (8-1)=40,7.
Pearsonin taulukkotesti 1 %:n merkitsevyystasolla on 18,5 ja 5 %:lla - 14,1..
Esimerkki osoittaa laskennan yksinkertaisuuden ja saavutettavuuden kaikille matemaattisten laskelmien perusteet tunteville. Niiden lievittämiseksi,käytä laskentataulukkolomakkeita.
Lopuksi
Siten yhteensopivuuskerroin osoittaa useiden asiantuntijoiden mielipiteiden johdonmukaisuuden. Mitä kauempana se on 0:sta ja lähempänä 1:tä, sitä johdonmukaisemmat mielipiteet ovat. Nämä kertoimet on vahvistettava laskemalla Pearson-kriteeri.






