Joskus näyttää siltä, että maailmamme on yksinkertainen ja selkeä. Itse asiassa tämä on maailmankaikkeuden suuri mysteeri, joka loi niin täydellisen planeetan. Tai ehkä sen on luonut joku, joka luultavasti tietää mitä tekee? Aikamme suurimmat mielet työskentelevät tämän kysymyksen parissa.

He tulevat joka kerta siihen tulokseen, että on mahdotonta luoda kaikkea, mitä meillä on ilman Korkeinta mieltä. Mikä poikkeuksellinen, monimutkainen ja samalla yksinkertainen ja suora maaplaneettamme! Maailma ympärillämme on hämmästyttävä säännöineen, muodoineen, väreineen.
Luonnon lait
Ensimmäinen asia, jonka huomaat v altavassa ja hämmästyttävässä planeetassamme, on aksiaalinen symmetria. Sitä esiintyy kaikissa muodoissa ympäröivästä maailmasta, ja se on myös kauneuden, ihanteellisuuden ja suhteellisuuden perusperiaate. Tämä ei ole muuta kuin matematiikkaa luonnossa.
Symmetrian käsite tarkoittaa harmoniaa, oikeellisuutta. Tämä on ympäröivän todellisuuden ominaisuus, joka systematisoi fragmentteja ja muuttaa ne yhdeksi kokonaisuudeksi. Jo muinaisessa Kreikassa tämän lain merkit alkoivat havaita ensimmäistä kertaa. Esimerkiksi Platon uskoi, että kauneus näkyy yksinomaansymmetrian ja suhteellisuuden vuoksi. Itse asiassa, jos katsomme esineitä, jotka ovat oikeasuhteisia, oikeita ja täydellisiä, sisäinen tilamme on kaunis.
Matematiikan lait elävässä ja elottomassa luonnossa
Katsotaanpa mitä tahansa olentoa, esimerkiksi täydellisintä - miestä. Näemme rungon rakenteen, joka näyttää sam alta molemmilta puolilta. Voit myös listata monia näytteitä, kuten hyönteisiä, eläimiä, meren elämää, lintuja. Jokaisella lajilla on oma värinsä.

Jos kuvioita tai kuvioita on olemassa, sen tiedetään peilautuvan keskiviivalla. Kaikki organismit syntyvät maailmankaikkeuden sääntöjen mukaan. Tällaisia matemaattisia kuvioita voidaan jäljittää elottomassa luonnossa.
Jos kiinnität huomiota kaikkiin ilmiöihin, kuten tornado, sateenkaari, kasvit, lumihiutaleet, voit löytää niistä paljon yhteistä. Symmetria-akselin suhteen puun lehti jaetaan kahtia, ja jokainen osa heijastaa edellistä.

Lisäksi, jos otamme esimerkiksi tornadon, joka nousee pystysuunnassa ja näyttää suppilolta, niin se voidaan myös ehdollisesti jakaa kahteen täysin identtiseen puolikkaaseen. Symmetria-ilmiön voi tavata päivän ja yön, vuodenaikojen vaihtuessa. Ympäröivän maailman lait ovat matematiikkaa luonnossa, jolla on oma täydellinen järjestelmänsä. Koko käsitys maailmankaikkeuden luomisesta perustuu siihen.
Sateenkaari
Ajattelemme harvoin luonnonilmiöitä. Satoi lunta tai satoi, katsoi ulosaurinko tai ukkonen iski - tavallinen muuttuvan sään tila. Harkitse moniväristä kaaria, joka löytyy yleensä sateen jälkeen. Sateenkaari taivaalla on hämmästyttävä luonnonilmiö, johon liittyy vain ihmissilmälle näkyvä kaikkien värien kirjo. Tämä tapahtuu, koska auringonsäteet kulkevat ulos lähtevän pilven läpi. Jokainen sadepisara toimii prismana, jolla on optisia ominaisuuksia. Voimme sanoa, että mikä tahansa pisara on pieni sateenkaari.

Vesisulun läpi kulkiessaan säteet muuttavat alkuperäistä väriään. Jokaisella valovirralla on tietty pituus ja sävy. Siksi silmämme havaitsee sateenkaaren sellaiseksi moniväriseksi. Huomaa mielenkiintoinen tosiasia, että tämän ilmiön voi nähdä vain henkilö. Koska se on vain illuusio.
Sateenkaaren tyypit
- Auringosta muodostuneet sateenkaaret ovat yleisimpiä. Se on kirkkain kaikista lajikkeista. Koostuu seitsemästä pääväristä: punainen oranssi, keltainen, vihreä, sininen, indigo, violetti. Mutta jos katsot yksityiskohtia, on olemassa paljon enemmän sävyjä kuin silmämme näkevät.
- Kuun luoma sateenkaari esiintyy yöllä. Uskotaan, että sen voi aina nähdä. Mutta kuten käytäntö osoittaa, periaatteessa tämä ilmiö havaitaan vain sateisilla alueilla tai suurten vesiputousten lähellä. Kuun sateenkaaren värit ovat hyvin himmeitä. Niitä on tarkoitus ottaa huomioon vain erikoislaitteiden avulla. Mutta jopa sen kanssa silmämme erottaa vain valkoisen kaistaleen.
- Sumun seurauksena ilmaantunut sateenkaari on kuin leveä kiiltävä valokaari. Joskus tämä tyyppi sekoitetaan edelliseen. Ylhäältä katsottuna väri voi olla oranssi, alha alta se voi olla violetin sävyinen. Auringon säteet, jotka kulkevat sumun läpi, muodostavat kauniin luonnonilmiön.
- Tuline sateenkaari taivaalla on erittäin harvinainen. Se ei ole samanlainen kuin edellinen laji vaakatasossa. Voit nähdä tämän ilmiön vain cirruspilvien yläpuolella. Ne ulottuvat yleensä 8-10 kilometrin korkeuteen. Kulman, jossa sateenkaari näyttää itsensä kaikessa loistossaan, on oltava yli 58 astetta. Värit pysyvät yleensä samoina kuin auringon sateenkaaressa.
Golden Ratio (1, 618)
Täydellinen osuus löytyy useimmiten eläinmaailmasta. Heille myönnetään sellainen osuus, joka on yhtä suuri kuin vastaavan PHI-luvun juuri yksi. Tämä suhde on kaikkien planeetan eläinten yhdistävä tosiasia. Antiikin suuret mielet kutsuivat tätä lukua jumalalliseksi suhteeksi. Sitä voidaan kutsua myös kultaiseksi leikkaukseksi.
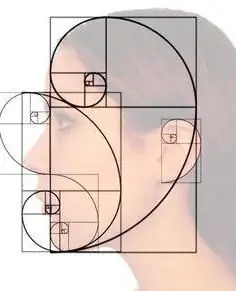
Tämä sääntö on täysin yhdenmukainen ihmisen rakenteen harmonian kanssa. Jos esimerkiksi määrität silmien ja kulmakarvojen välisen etäisyyden, se on yhtä suuri kuin jumalallinen vakio.
Kultainen leikkaus on esimerkki matematiikan merkityksestä luonnossa, jonka lakia suunnittelijat, taiteilijat, arkkitehdit, kauniiden ja täydellisten asioiden luojat alkoivat noudattaa. He luovat jumalallisen vakion avulla luomuksiaan, jotka ovat tasapainoisia, harmonisia ja miellyttäviä katsella. Mielemme voi laskeakauniita ovat ne asiat, esineet, ilmiöt, joissa osien suhde on epätasainen. Suhteellisuus on se, mitä aivomme kutsuvat kultaiseksi leikkaukseksi.
DNA-helix
Kuten saksalainen tiedemies Hugo Weil aivan oikein totesi, symmetrian juuret tulivat matematiikan kautta. Monet panivat merkille geometristen kuvioiden täydellisyyden ja kiinnittivät niihin huomiota. Esimerkiksi hunajakenno ei ole muuta kuin luonnon itsensä luoma kuusikulmio. Voit myös kiinnittää huomiota kuusen käpyihin, joilla on lieriömäinen muoto. Myös spiraali löytyy usein ulkomaailmasta: suurten ja pienten eläinten sarvet, äyriäisten kuoret, DNA-molekyylejä.

DNA-kierre on luotu kultaisen leikkauksen periaatteen mukaisesti. Se on linkki materiaalin rakenteen ja sen todellisen kuvan välillä. Ja jos ajattelemme aivoja, ne eivät ole muuta kuin johdin kehon ja mielen välillä. Äly yhdistää elämän ja sen ilmenemismuodon ja antaa muodon sisältämän elämän tuntea itsensä. Tämän avulla ihmiskunta voi ymmärtää ympäröivää planeettaa, etsiä siitä malleja, joita sitten sovelletaan sisäisen maailman tutkimiseen.
Fissio luonnossa
Solumitoosi koostuu neljästä vaiheesta:
- Prophase. Se lisää ydintä. Näkyviin tulee kromosomeja, jotka alkavat kiertyä spiraaliksi ja muuttuvat tavalliseen muotoonsa. Paikka muodostuu solujen jakautumiselle. Vaiheen lopussa ydin ja sen kalvo liukenevat ja kromosomit virtaavat sytoplasmaan. Tämä on pisin jakovaihe.
- Metafaasi. Täällä kromosomien kiertyminen spiraaliksi päättyy, ne muodostavat metafaasilevyn. Kromatidit asettuvat toisiaan vastapäätä valmistautuessaan jakautumiseen. Niiden välissä on paikka katkaisulle - kara. Tämä päättää toisen vaiheen.
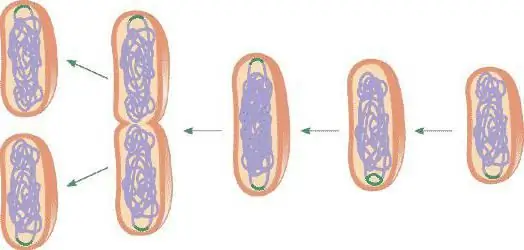
- Anafaasi. Kromatidit liikkuvat vastakkaisiin suuntiin. Nyt solussa on kaksi sarjaa kromosomeja niiden jakautumisen vuoksi. Tämä vaihe on hyvin lyhyt.
- Telofaasi. Solun jokaiseen puoliskoon muodostuu ydin, jonka sisällä muodostuu tuma. Sytoplasma dissosioituu aktiivisesti. Kara katoaa vähitellen.
Mitoosin merkitys
Ainutlaatuisen jakautumismenetelmän ansiosta jokaisella seuraavalla solulla on lisääntymisen jälkeen sama geenikoostumus kuin sen emolla. Molempien solujen kromosomien koostumus vastaanottaa saman. Se ei tullut toimeen ilman sellaista tiedettä kuin geometria. Mitoosin eteneminen on tärkeää, koska kaikki solut lisääntyvät tämän periaatteen mukaisesti.
Mistä mutaatiot tulevat
Tämä prosessi takaa jatkuvan joukon kromosomeja ja geneettisiä materiaaleja jokaisessa solussa. Mitoosin vuoksi tapahtuu organismin kehitystä, lisääntymistä ja uudistumista. Joidenkin myrkkyjen vaikutuksesta johtuvassa solunjakautumisen häiriössä kromosomit eivät välttämättä hajoa puolikkaiksi tai niissä voi ilmetä rakenteellisia häiriöitä. Tämä on selvä osoitus alkavista mutaatioista.
Yhteenveto
Mitä yhteistä on matematiikalla ja luonnolla? Löydät vastauksen tähän kysymykseen artikkelistamme. Ja jos kaivaa syvemmälle, tarvitsetsanoa, että ympäröivää maailmaa tutkimalla ihminen tuntee itsensä. Ilman Korkeinta mieltä, joka synnytti kaiken elävän, mitään ei olisi voinut tapahtua. Luonto on yksinomaan harmoniassa, tiukassa lakiensa järjestyksessä. Onko tämä kaikki mahdollista ilman syytä?
Laitataan tiedemies, filosofi, matemaatikon ja fyysikon Henri Poincarén lausunto, joka, kuten kukaan muu, pystyy vastaamaan kysymykseen siitä, onko matematiikka luonnossa perustavanlaatuista. Jotkut materialistit eivät ehkä pidä tällaisesta päättelystä, mutta he eivät todennäköisesti pysty kumoamaan sitä. Poincaré sanoo, että harmoniaa, jonka ihmismieli haluaa löytää luonnosta, ei voi olla sen ulkopuolella. Objektiivinen todellisuus, joka on läsnä ainakin muutaman yksilön mielessä, voi olla koko ihmiskunnan ulottuvilla. Yhteyttä, joka kokoaa yhteen henkisen toiminnan, kutsutaan maailman harmoniaksi. Viime aikoina tällaisen prosessin tiellä on edistytty v altavasti, mutta ne ovat hyvin pieniä. Näiden maailmankaikkeuden ja yksilön yhdistävien linkkien pitäisi olla arvokkaita kaikille ihmismielelle, joka on herkkä näille prosesseille.






