Matematiikassa summaus (merkitty suurella kreikkalaisella sigmasymbolilla) on joukko lukujen yhteenlaskuja. Mikä on summa? Tämä on seurausta tällaisesta toiminnasta. Jos luvut lasketaan yhteen peräkkäin vasemm alta oikealle, niin välitulos on osasumma.
Mikä on summa?
Summoitavat luvut voivat olla kokonaislukuja, rationaalisia, todellisia tai kompleksisia. Niiden lisäksi voidaan lisätä muun tyyppisiä arvoja: vektoreita, matriiseja, polynomeja ja yleensä minkä tahansa additiivisen ryhmän (tai jopa monoidin) elementtejä.
Jos termien elementtien lukumäärä on äärellinen, niin summaus antaa aina hyvin määritellyn arvon. Äärettömän arvojen summausta kutsutaan sarjaksi. Sen arvo voidaan usein määrittää käyttämällä rajaa (vaikka joskus arvo voi olla ääretön).
Sequences
Lukujen [3, 7, 2, 1] summaus voidaan määrittää lausekkeella, jonka arvo on siihen sisältyvien numeroiden summa, esimerkiksi 3 + 7 + 2 + 1=13. Koska lisäysassosiatiivisesti summa ei riipu termien ryhmittelystä, esimerkiksi (3 + 7) + (2 + 1) ja 3 + ((7 + 2) + 1) ovat molemmat yhdeksän, joten sulkuja ei yleensä tarvitse käyttää. Myös yhteenlasku on kommutatiivista, joten termien uudelleenjärjestely ei muuta summan arvoa. Huomaa, että tämä ominaisuus ei välttämättä toimi äärettömässä summauksessa.

Tällaisten sekvenssien summaamiseen ei ole erityistä merkintää. On vain pieni vivahde, jos elementtejä on vähemmän kuin kaksi. Yhden jäsenen sekvenssin summa ei sisällä plusmerkkiä (se ei erotu itse luvun muodosta), ja jos elementtejä ei ole ollenkaan, sitä ei voi edes kirjoittaa (mutta sen sijaan sitä voidaan merkitä sen arvo "0"). Jos kuitenkin sekvenssin ehdot määritellään tietyllä kuviolla, kuten funktiolla, summausoperaattori voi olla hyödyllinen tai jopa välttämätön.
Ennätys
Ymmärtääksesi, mikä summa on, on myös tarpeen jäsentää sen ulkonäkö.
Kokolukujen sekvenssin summaamiseksi 1:stä 100:aan käytetään usein lauseketta, joka sisältää ellipsin osoittamaan puuttuvat jäsenet: 1 + 2 + 3 + 4 + … + 99 + 100. Malli on melko helppo nähdä tässä esimerkissä. Monimutkaisempia vaihtoehtoja varten on kuitenkin tarpeen määrittää täsmälleen se sääntö, jota käytetään elementtien arvon löytämiseen, mikä voidaan saavuttaa "Σ" -summausoperaattorilla. Tällä symbolilla (sigma) voit käyttää seuraavaa merkintää:
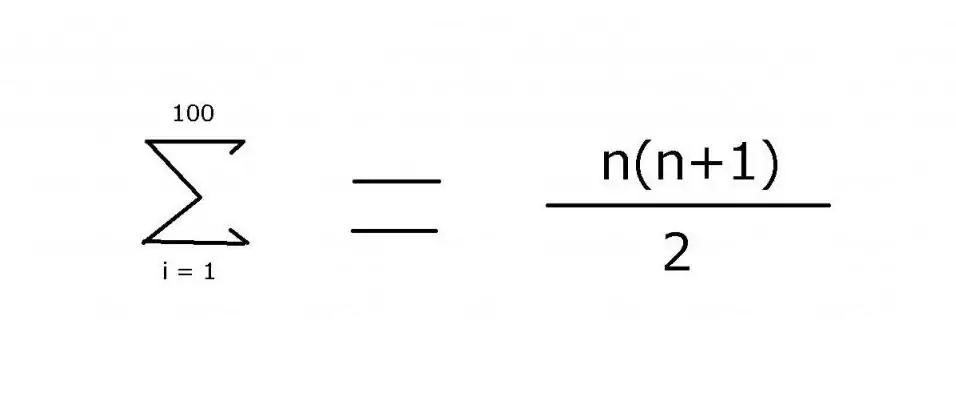
Tämän lausekkeen arvo on 5050. Se voidaan löytää käyttämällä matemaattista induktiota, josta kaavan toinen osa tulee.
Kaava muuttuu eri sarjoissa. Tallennusprosessi rajoittuu jonkin äärettömän sekvenssin esikuvan etsimiseen ja sen sitten kuvaamiseen kaavalla. Tämän jälkeen ei ole vaikeaa ymmärtää, mikä summa on tietyssä tapauksessa.
Kun on tarpeen selventää, että luvut lasketaan yhteen niiden etumerkeineen (plus tai miinus), käytetään termiä algebrallinen summa. Esimerkiksi sähköpiiriteoriassa Kirchhoffin piirilait ottavat huomioon virtojen algebrallisen summan johtimien verkossa, jotka kohtaavat jossain pisteessä, antaen päinvastaiset merkit solmuun sisään ja sieltä lähteville virroille.






