On olemassa kaikenlaisia mekaanisia laitteita. Jotkut heistä ovat meille tuttuja lapsuudesta lähtien. Näitä ovat esimerkiksi kellot, polkupyörät, kehrät. Opimme toisista vanhetessamme. Nämä ovat autojen moottoreita, nostureiden vinssejä ja muita. Jokainen liikkuva mekanismi käyttää jonkinlaista järjestelmää saadakseen pyörät pyörimään ja koneen toimimaan. Yksi mielenkiintoisimmista ja suosituimmista on planeettamekanismi. Sen ydin on siinä, että konetta ohjaavat pyörät tai vaihteet, jotka ovat vuorovaikutuksessa toistensa kanssa erityisellä tavalla. Katsotaanpa sitä tarkemmin.
Yleistä tietoa
Planeettapyörä ja planeettamekanismi on nimetty näin analogisesti aurinkokuntamme kanssa, joka voidaan esittää ehdollisesti seuraavasti: keskellä on "aurinko" (mekanismin keskipyörä). "Planeetat" (pienet pyörät tai satelliitit) liikkuvat sen ympärillä. Kaikissa näissä planeettavaihteiston osissa on ulkoiset hampaat. Ehdollisen aurinkokunnan halkaisijalla on raja. Roolise suoritetaan planeettamekanismissa suurella pyörällä tai episyklillä. Siinä on myös hampaat, vain sisäiset. Suurin osa tämän mallin työstä suorittaa kantolaite, joka on vipumekanismi. Liikkuminen voidaan suorittaa eri tavoin: joko aurinko pyörii tai jakso, mutta aina yhdessä satelliittien kanssa.
Planeettamekanismin toiminnan aikana voidaan käyttää toista mallia, esimerkiksi kahta aurinkoa, satelliittia ja kantoa altoa, mutta ilman episykliä. Toinen vaihtoehto on kaksi episykliä, mutta ilman aurinkoa. Kantoaallon ja satelliittien on aina oltava läsnä. Pyörien lukumäärästä ja niiden pyörimisakseleiden sijainnista avaruudessa riippuen muotoilu voi olla yksinkertainen tai monimutkainen, tasainen tai tilallinen.
Ymmärtääksesi täysin, kuinka tällainen järjestelmä toimii, sinun on ymmärrettävä yksityiskohdat.
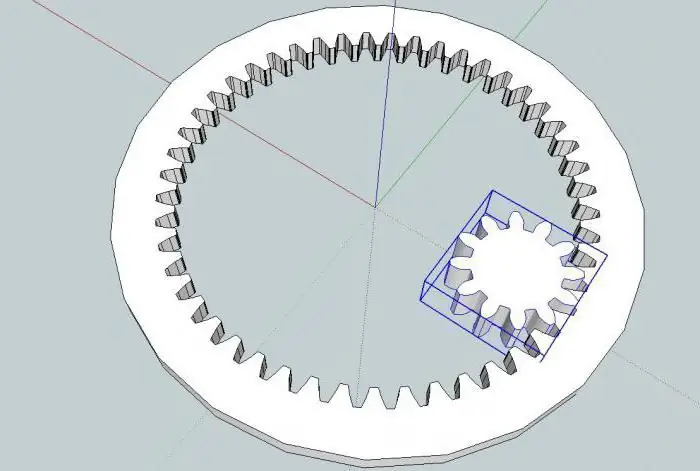
Elementtien sijainti
Planeettavaihteiston yksinkertaisin muoto sisältää kolme vaihdesarjaa, joiden vapausaste vaihtelee. Yllä olevat satelliitit pyörivät akselinsa ympäri ja samalla auringon ympäri, joka pysyy paikallaan. Episykli yhdistää planeettamekanismin ulkopuolelta ja myös pyörii hampaiden (se ja satelliitit) vuorottelun avulla. Tämä malli pystyy muuttamaan vääntömomenttia (kulmanopeuksia) yhdessä tasossa.
Yksinkertaisessa planeettamekanismissa aurinko ja satelliitit voivat pyöriä, mutta episentrumi pysyy kiinteänä. Joka tapauksessa kaikkien komponenttien kulmanopeudet eivät ole kaoottisia, vaan niillä on lineaarinen riippuvuus toisistaan. Kun media pyörii, se tarjoaaalhainen nopeus korkea vääntömomentti.
Eli planeettavaihteiston ydin on, että tällainen rakenne pystyy muuttamaan, laajentamaan ja lisäämään vääntömomenttia ja kulmanopeutta. Pyörimisliikkeet tapahtuvat tässä tapauksessa yhdellä geometrisellä akselilla. Eri ajoneuvojen ja mekanismien tarvittava vaihteistoelementti on asennettu.

Rakennemateriaalien ja kaavioiden ominaisuudet
Kiinteää komponenttia ei kuitenkaan aina tarvita. Differentiaalijärjestelmissä jokainen elementti pyörii. Tämän k altaisissa planeettavaihteissa on yksi lähtöohjattu (ohjaava) kaksi tuloa. Esimerkiksi tasauspyörästö, joka ohjaa auton akselia, on samanlainen vaihde.
Tällaiset järjestelmät toimivat samalla periaatteella kuin rinnakkaiset akselirakenteet. Jopa yksinkertaisessa planeettapyörästössä on kaksi tuloa, kiinteä rengashammaspyörä on vakiotulo, jonka kulmanopeus on nolla.
Yksityiskohtainen kuvaus laitteista
Mikroplaneettarakenteissa voi olla eri määrä pyöriä sekä eri vaihteita, joiden kautta ne on kytketty. Tällaisten yksityiskohtien läsnäolo laajentaa suuresti mekanismin mahdollisuuksia. Komposiittiset planeettarakenteet voidaan koota siten, että alustan akseli liikkuu suurella nopeudella. Tämän seurauksena jotkin alennusvaihteiden, aurinkovaihteiden ja muiden ongelmista voidaan poistaa laitetta parannettaessa.
Näin, kuten näkyyTietojen perusteella planeettamekanismi toimii periaatteella siirtää pyörimistä keskeisten ja liikkuvien linkkien välillä. Samaan aikaan monimutkaiset järjestelmät ovat enemmän kysyttyjä kuin yksinkertaiset.
Määritysasetukset
Planettamekanismissa on mahdollista käyttää eri kokoonpanojen pyöriä (vaihteita). Sopiva standardi suorilla hampailla, kierteellä, matolla, chevronilla. Sitoutumisen tyyppi ei vaikuta planeettamekanismin yleiseen toimintaperiaatteeseen. Tärkeintä on, että kannattimen ja keskipyörien pyörimisakselit ovat samat. Mutta satelliittien akselit voivat sijaita muilla tasoilla (risteävät, yhdensuuntaiset, leikkaavat). Esimerkki ristikkäisestä on pyörien välinen tasauspyörästö, jossa vaihteet ovat kartiomaisia. Esimerkki ristikkäisestä on itselukkiutuva tasauspyörästö kierukkavaihteella (Torsen).
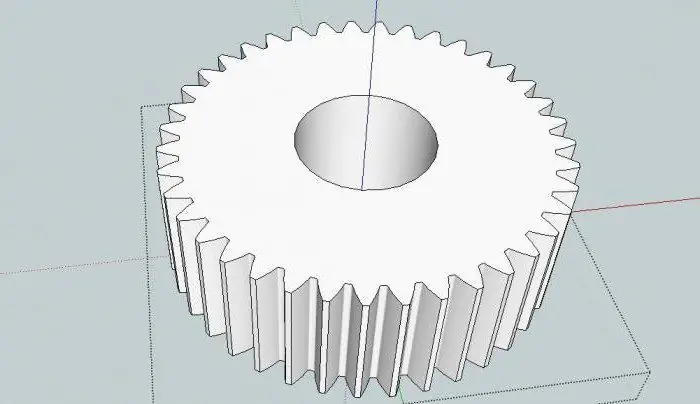
Yksinkertaiset ja monimutkaiset laitteet
Kuten yllä todettiin, planeettamekanismin kaavio sisältää aina kannakkeen ja kaksi keskipyörää. Satelliitteja voi olla mikä tahansa määrä. Tämä on niin kutsuttu yksinkertainen tai peruslaite. Tällaisissa mekanismeissa mallit voivat olla seuraavat: "SVS", "SVE", "EVE", missä:
- S on aurinko.
- B - operaattori.
- E on episentrumi.
Jokaista tällaista pyörää + satelliitteja kutsutaan planeettavaihteistoksi. Tässä tapauksessa kaikkien pyörien on pyörittävä samassa tasossa. Yksinkertaiset mekanismit ovat yksi- ja kaksirivisiä. Niitä käytetään harvoin erilaisissa teknisissä laitteissa ja koneissa. Esimerkkivoi toimia planeettapyörämekanismina. Tämän periaatteen mukaan holkki toimii, minkä ansiosta liike suoritetaan. Sen suunnittelu luotiin "SVE" -järjestelmän mukaan. Satelliitteja ei neljässä kappaleessa. Tässä tapauksessa aurinko on kiinnitetty tiukasti takapyörän akseliin ja episentrumi on liikkuva. Pyöräilijä pakottaa sen pyörimään polkimia painamalla. Tässä tapauksessa lähetysnopeus ja siten pyörimisnopeus voivat muuttua.
Useammin voit löytää monimutkaisia vaihteistoplaneettamekanismeja. Niiden järjestelmät voivat olla hyvin erilaisia, mikä riippuu siitä, mihin tämä tai tuo malli on tarkoitettu. Yleensä monimutkaiset mekanismit koostuvat useista yksinkertaisista mekanismeista, jotka on luotu planeettavaihteiston yleissäännön mukaisesti. Tällaiset monimutkaiset järjestelmät ovat kaksi-, kolmi- tai nelirivisiä. Teoriassa on mahdollista luoda rakenteita, joissa on suuri määrä rivejä, mutta käytännössä näin ei tapahdu.
Taso- ja tilalaitteet
Jotkut ihmiset ajattelevat, että yksinkertaisen planeettavaihteen on oltava litteä. Tämä on vain osittain totta. Monimutkaiset laitteet voivat olla myös litteitä. Tämä tarkoittaa, että planeettavaihteet, riippumatta siitä kuinka montaa niitä laitteessa käytetään, ovat yhdessä tai rinnakkaisissa tasoissa. Tilamekanismeissa on planeettavaihteet kahdessa tai useammassa tasossa. Tässä tapauksessa itse pyörät voivat olla pienempiä kuin ensimmäisessä suoritusmuodossa. Huomaa, että litteä planeettamekanismi on sama kuin spatiaalinen. Ero on vain laitteen käytössä olevassa alueella, eli kompaktissa.
Vapausasteet
Tämä on kokoelman nimipyörimiskoordinaatit, joiden avulla voit määrittää järjestelmän sijainnin avaruudessa tietyllä hetkellä. Itse asiassa jokaisella planeettamekanismilla on vähintään kaksi vapausastetta. Toisin sanoen minkään tällaisten laitteiden lenkkien pyörimiskulmanopeudet eivät ole lineaarisesti yhteydessä toisiinsa, kuten muissa vaihteissa. Tämän avulla voit saada ulostulon kulmanopeuksia, jotka eivät ole samat kuin tulon kulmanopeudet. Tämä voidaan selittää sillä, että planeettamekanismin differentiaaliyhteydessä missä tahansa rivissä on kolme elementtiä, ja loput yhdistetään siihen lineaarisesti, minkä tahansa rivin elementin kautta. Teoriassa on mahdollista luoda planeettajärjestelmiä kolmella tai useammalla vapausasteella. Mutta käytännössä ne ovat käyttökelvottomia.

Planeetaarinen välityssuhde
Tämä on pyörivän liikkeen tärkein ominaisuus. Sen avulla voit määrittää, kuinka monta kertaa vetoakseliin kohdistuva voimamomentti on kasvanut suhteessa käyttöakselin momenttiin. Voit määrittää välityssuhteen käyttämällä kaavoja:
i=d2/d1=Z2/Z1=M2/M1=W1/W2=n1/n2, missä:
- 1 - johtava linkki.
- 2 - orjalinkki.
- d1, d2 - ensimmäisen ja toisen linkin halkaisijat.
- Z1, Z2 - hampaiden lukumäärä.
- M1, M2 ovat vääntömomentteja.
- W1 W2 - kulmanopeudet.
- n1 n2 - nopeus.
Siksi, kun välityssuhde on suurempi kuin yksi vetoakselilla, voimamomentti kasvaa ja taajuus ja kulmanopeus pienenevät. Tämä tulee aina ottaa huomioon suunnittelua luotaessa, koskaplaneettamekanismien välityssuhde riippuu siitä, kuinka monta hammasta pyörissä on ja mikä rivin elementti on johtava.
Soveltamisala
Nykyajan maailmassa on monia erilaisia koneita. Monet niistä toimivat planeettavaihteiden avulla.
Niitä käytetään autojen tasauspyörästöissä, planeettavaihteissa, monimutkaisten työstökoneiden kinemaattisissa järjestelmissä, lentokoneiden ilmamoottorien vaihteistoissa, polkupyörissä, puimureissa ja traktoreissa, tankeissa ja muissa sotilasvarusteissa. Planeettavaihteiston periaatteiden mukaan monet vaihteistot toimivat sähkögeneraattoreiden käyttöissä. Harkitse toista tällaista järjestelmää.
Planeettinen kääntövaihde
Tätä mallia käytetään joissakin traktoreissa, tela-ajoneuvoissa ja säiliöissä. Yksinkertainen kaavio laitteesta on esitetty alla olevassa kuvassa.
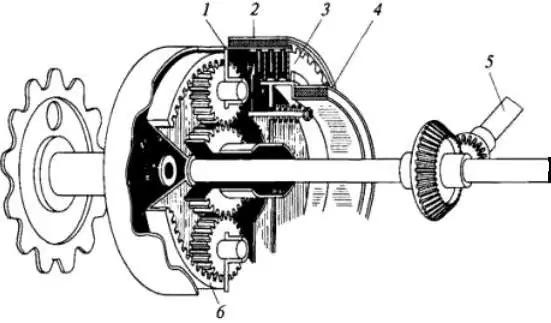
Planettakiertomekanismin toimintaperiaate on seuraava: kannatin (asento 1) on kytketty jarrurumpuun (2) ja telaketjussa sijaitsevaan käyttöpyörään. Episykli (6) on kytketty voimansiirtoakseliin (asento 5). Aurinko (8) on kytketty kytkinlevyyn (3) ja kääntöjarrurumpuun (4). Kun lukituskytkin on kytkettynä ja nauhajarrut on kytketty pois päältä, satelliitit eivät pyöri. Niistä tulee kuin vipuja, koska ne on yhdistetty aurinkoon (8) ja episykliin (6) hampaiden avulla. Siksi ne pakottavat ne ja kannattimen samanaikaisesti pyörimään yhteisen akselin ympäri. Tässä tapauksessa kulmanopeus on sama.
Kun lukituskytkin irrotetaan ja jarru painetaanauringon kääntäminen alkaa pysähtyä ja satelliitit alkavat liikkua akseliensa ympäri. Siten ne luovat hetken telineeseen ja pyörittävät telaketjun vetopyörää.
Wear
Käyttöiän ja vaimennuksen os alta lineaarisissa planeettajärjestelmissä kuormituksen jakautuminen on havaittavissa pääkomponenttien kesken.
Lämpö- ja syklinen väsymys voi lisääntyä niissä johtuen rajoitetusta kuorman jakautumisesta ja siitä, että planeettapyörät voivat pyöriä melko nopeasti akseleillaan. Lisäksi planeettavaihteen suurilla nopeuksilla ja välityssuhteilla keskipakovoimat voivat lisätä liikkeen määrää huomattavasti. On myös huomattava, että kun tuotannon tarkkuus heikkenee ja satelliittien määrä lisääntyy, epätasapainon taipumus kasvaa.
Nämä laitteet ja niiden järjestelmät voivat jopa olla alttiina kulumiselle. Jotkut mallit ovat herkkiä pienillekin epätasapainoille ja saattavat vaatia laadukkaita ja kalliita kokoonpanokomponentteja. Planeetatappien tarkka sijainti aurinkopyörän akselin ympärillä voi olla ratkaiseva tekijä.
Muihin planeettajärjestelyihin, jotka auttavat tasapainottamaan kuormia, kuuluvat kelluvien osakokoonpanojen tai "pehmeiden" kiinnikkeiden käyttö pitämään aurinko tai episentrumi liikkeessä mahdollisimman pitkään.

Planeettalaitteiden synteesin perusteet
Tätä tietoa tarvitaan konekomponenttien suunnittelussa ja luomisessa. "Planeettamekanismien synteesin" käsite on hampaiden lukumäärän laskeminenauringossa, episentrumissa ja satelliiteissa. Tässä tapauksessa useiden ehtojen on täytyttävä:
- Välityssuhteen on oltava sama kuin asetettu arvo.
- Hammaspyörän hampaiden kytkennän on oltava oikea.
- On tarpeen varmistaa tuloakselin ja ulostuloakselin kohdistus.
- Naapuri vaaditaan (satelliitit eivät saa häiritä toisiaan).
Myös suunnittelussa tulee ottaa huomioon tulevan rakenteen mitat, paino ja tehokkuus.
Jos välityssuhde (n) on annettu, niin auringon (S) ja planeettavaihteiden (P) hampaiden lukumäärän on täytettävä yhtälö:
n=S/P
Jos oletamme, että hampaiden lukumäärä episentrumissa on varhainen (A), niin kantolaitteen ollessa lukittuna tulee noudattaa yhtäläisyyttä:
n=-S/A
Jos episentrumi on kiinteä, seuraava yhtälö on totta:
n=1+ A/S
Näin planeettamekanismi lasketaan.

Edut ja haitat
On olemassa useita siirtotyyppejä, joita käytetään menestyksekkäästi eri laitteissa. Planetary niiden joukossa erottuu seuraavista eduista:
- Antaa vähemmän kuormitusta pyörien jokaiselle hampaalle (sekä aurinko, episentrumi ja satelliitit), koska niihin kohdistuva kuormitus jakautuu tasaisemmin. Tällä on positiivinen vaikutus rakenteen käyttöikään.
- Samalla teholla planeettavaihteistolla on pienemmät mitat ja paino kuin muilla voimansiirtotyypeillä.
- Mahdollisuus saavuttaa korkeammat välityssuhteetvähemmän pyöriä.
- Varmista vähemmän melua.
Planeettavaihteiden haitat:
- Valmistamiseen tarvitaan lisää tarkkuutta.
- Matala hyötysuhde suhteellisen suurella välityssuhteella.






