Kaasut, termodynamiikan näkökulmasta, kuvataan joukolla makroskooppisia ominaisuuksia, joista tärkeimmät ovat lämpötila, paine ja tilavuus. Yhden näistä parametreista pysyvyys ja muutos kahdessa muussa osoittaa, että yksi tai toinen isoprosessi tapahtuu kaasussa. Omistamme tämän artikkelin yksityiskohtaiseen vastaukseen kysymyksiin, että tämä on isokorinen prosessi, miten se eroaa isotermisistä ja isobarisista muutoksista kaasujärjestelmän tiloissa.
Ihanteellinen kaasu fysiikassa

Ennen kuin vastaat kysymykseen, että tämä on isokorinen prosessi, sinun tulee tutustua ideaalikaasun käsitteeseen paremmin. Fysiikassa sillä tarkoitetaan mitä tahansa kaasua, jossa sen muodostavien hiukkasten keskimääräinen kineettinen energia ylittää huomattavasti niiden vuorovaikutuksen potentiaalisen energian ja näiden hiukkasten väliset etäisyydet ovat useita suuruusluokkaa suurempia kuin niiden lineaariset mitat. Mainituissa olosuhteissa se on mahdollista suoritettaessalaskelmissa ei oteta huomioon hiukkasten välistä vuorovaikutusenergiaa (se on yhtä kuin nolla), ja voidaan myös olettaa, että hiukkaset ovat ainepisteitä, joilla on tietty massa m.
Ainoa prosessi, joka tapahtuu ihanteellisessa kaasussa, on hiukkasten törmäys ainetta sisältävän astian seiniin. Nämä törmäykset ilmenevät käytännössä tietyn paineen olemassaolona kaasussa P.
Yleensä mitä tahansa kaasumaista ainetta, joka koostuu kemiallisesti suhteellisen inertistä molekyyleistä ja jolla on alhainen paine ja korkea lämpötila, voidaan pitää ihanteellisena kaasuna riittävän tarkasti käytännön laskelmia varten.
Yhtälö, joka kuvaa ihanteellista kaasua
Tietenkin puhumme Clapeyron-Mendelejevin universaalista laista, joka pitäisi ymmärtää hyvin ymmärtääkseen, että tämä on isokorinen prosessi. Joten universaalilla tilayhtälöllä on seuraava muoto:
PV=nRT.
Toisin sanoen paineen P ja kaasutilavuuden V tulo on yhtä suuri kuin absoluuttisen lämpötilan T ja aineen määrän tulo mooliina n, missä R on suhteellisuustekijä. Itse yhtälön kirjoitti ensimmäisen kerran Emile Clapeyron vuonna 1834, ja 1800-luvun 70-luvulla D. Mendelejev korvasi siinä joukon yhden yleisen kaasuvakion R (8,314 J/(molK) vakioarvoja.)).
Clapeyron-Mendeleevin yhtälön mukaisesti suljetussa järjestelmässä kaasuhiukkasten määrä pysyy vakiona, joten makroskooppisia parametreja on vain kolme, jotka voivat muuttua (T, Pja V). Jälkimmäinen tosiasia on eri isoprosessien ymmärtämisen taustalla, joita käsitellään jäljempänä.
Mikä on isokorinen prosessi?
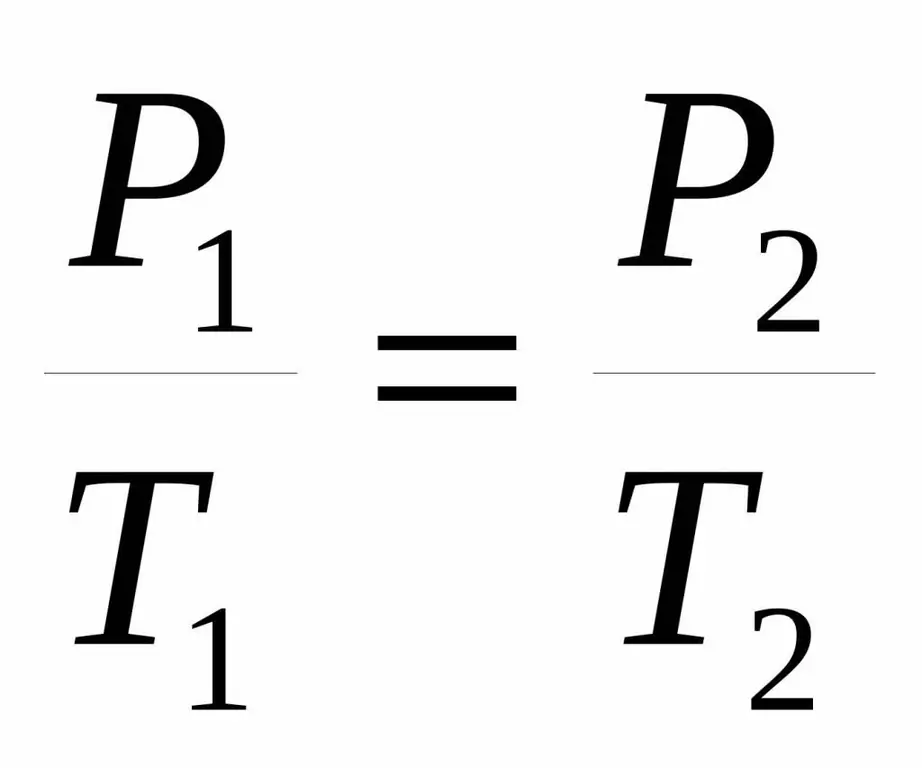
Tällä prosessilla tarkoitetaan mitä tahansa muutosta järjestelmän tilassa, jossa sen tilavuus säilyy.
Jos käännytään yleismaailmalliseen tilayhtälöön, voidaan sanoa, että isokorisessa prosessissa vain paine ja absoluuttinen lämpötila muuttuvat kaasussa. Ymmärtääksemme tarkasti, kuinka termodynaamiset parametrit muuttuvat, kirjoitamme vastaavan matemaattisen lausekkeen:
P / T=vakio
Joskus tämä yhtäläisyys annetaan hieman eri muodossa:
P1 / T1=P2 / T 2.
Molempia yhtäläisyyksiä kutsutaan Charlesin laiksi ranskalaisen tiedemiehen nimen mukaan, joka 1700-luvun lopulla sai mainitun riippuvuuden kokeellisesti.

Jos rakennamme funktion P(T) graafin, saadaan suorariippuvuus, jota kutsutaan isokoriksi. Mikä tahansa isokori (kaikille n:n ja V:n arvoille) on suora.
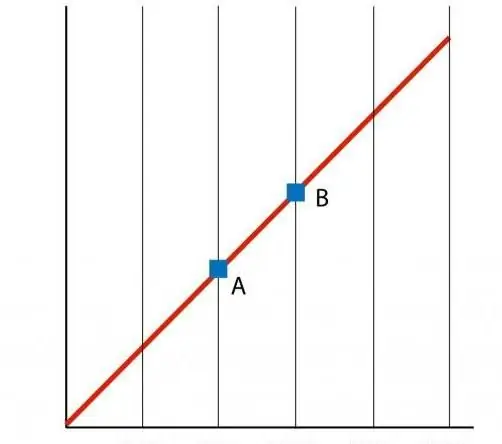
Prosessin energiakuvaus
Kuten todettiin, isokorinen prosessi on muutos järjestelmän tilassa, joka tapahtuu suljetussa mutta ei eristetyssä järjestelmässä. Puhumme mahdollisesta lämmönvaihdosta kaasun ja ympäristön välillä. Yleensä mikä tahansa lämmön Q syöttäminen järjestelmään johtaa kahteen tulokseen:
- muuttaa sisäistä energiaa U;
- kaasutoimii A, laajentaa tai supistaa.
Viimeinen johtopäätös kirjoitetaan matemaattisesti seuraavasti:
Q=U + A.
Ideaalikaasun isokorinen prosessi ei määritelmänsä mukaan tarkoita kaasun suorittamaa työtä, koska sen tilavuus pysyy muuttumattomana. Tämä tarkoittaa, että kaikki järjestelmään syötetty lämpö menee sen sisäisen energian lisäämiseen:
Q=U.
Jos korvaamme tämän lausekkeen sisäisen energian eksplisiittisen kaavan, isokorisen prosessin lämpö voidaan esittää seuraavasti:
Q=z / 2nRT.
Tässä z on vapausasteiden lukumäärä, joka määräytyy kaasun muodostavien molekyylien polyatomisen luonteen mukaan. Yksiatomiselle kaasulle z=3, kaksiatomiselle kaasulle - 5 ja kolmiatomiselle ja useammalle - 6. Tässä vapausasteiden alla tarkoitamme translaatio- ja rotaatioasteita.
Jos vertaamme kaasujärjestelmän lämmityksen tehokkuutta isokorisissa ja isobarisissa prosesseissa, niin ensimmäisessä tapauksessa saamme maksimaalisen hyötysuhteen, koska järjestelmän tilan isobarisen muutoksen aikana kaasu laajenee ja osa lämmöstä kuluu työntekoon.
Isobaarinen prosessi
Yllä olemme kuvanneet yksityiskohtaisesti, että tämä on isokorinen prosessi. Sanotaan nyt muutama sana muista isoprosesseista. Aloitetaan isobaarista. Nimen perusteella se ymmärretään järjestelmän siirtymäksi tilojen välillä vakiopaineessa. Tämä prosessi kuvataan Gay-Lussacin laissa seuraavasti:
V / T=vakio
Isokorin tapaan V(T)-isopalkki edustaa myös kaaviossa suoraa viivaa.
Siitämistä tahansa isobarisesta prosessista on kätevää laskea kaasun tekemä työ, koska se on yhtä suuri kuin vakiopaineen ja tilavuuden muutoksen tulo.
Isoterminen prosessi
Tämä on prosessi, jossa järjestelmän lämpötila pysyy vakiona. Sitä kuvaa Boyle-Mariotte-laki ihanteelliselle kaasulle. On mielenkiintoista huomata, että tämä on ensimmäinen kokeellisesti löydetty kaasulaki (1600-luvun toinen puoli). Sen matemaattinen merkintätapa näyttää tältä:
PV=vakio
Isokoriset ja isotermiset prosessit eroavat toisistaan graafisen esityksensä suhteen, koska funktio P(V) on hyperbolinen, ei lineaarinen suhde.
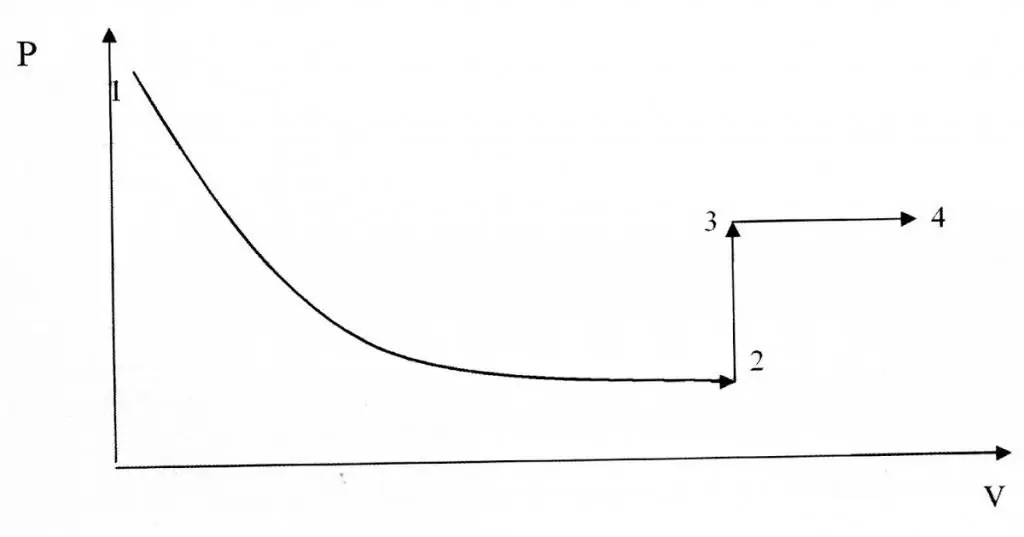
Esimerkki ongelmanratkaisusta
Kohdistetaan artikkelissa esitetyt teoreettiset tiedot niiden sovelluksilla käytännön ongelman ratkaisemiseksi. Tiedetään, että puhdasta kaasumaista typpeä oli sylinterissä 1 ilmakehän paineessa ja 25 °C:n lämpötilassa. Kaasusylinterin kuumentamisen ja paineen mittaamisen jälkeen se osoittautui 1,5 ilmakehän paineeksi. Mikä on kaasun lämpötila sylinterissä lämmityksen jälkeen? Kuinka paljon kaasun sisäenergia muuttui, jos ilmapallossa oli 4 moolia typpeä.
Vastaaksemme ensimmäiseen kysymykseen käytämme seuraavaa lauseketta:
P1 / T1=P2 / T 2.
Mistä saamme:
T2=P2 / P1 T 1.
Tässä lausekkeessa paine voidaan korvata mieliv altaisilla yksiköillämittaukset, koska ne kutistuvat, ja lämpötila on vain kelvineissä. Tämän jälkeen saamme:
T2=1,5 /1298,15=447,224 K.
Laskettu lämpötila celsiusasteina on 174 °C.
Koska typpimolekyyli on kaksiatominen, voidaan sen sisäisen energian muutos lämmityksen aikana määrittää seuraavasti:
ΔU=5/2nRΔT.
Korvaamalla tunnetut arvot tähän lausekkeeseen, saamme vastauksen ongelman toiseen kysymykseen: ΔU=+12,4 kJ.






